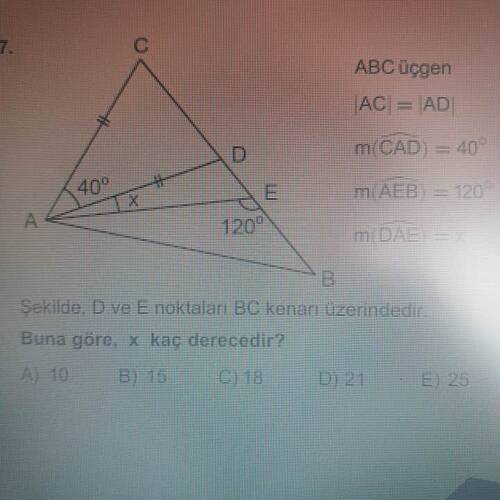
Şekilde, D ve E noktaları BC kenarı üzerindedir. Buna göre, x kaç derecedir?
Verilenleri özümseyerek başlayalım:
- AC = AD: Bu, \triangle ACD 'nin ikizkenar üçgen olduğunu gösterir.
- m(\angle CAD) = 40^\circ
- \angle AEB = 120^\circ
İlk olarak, \triangle ACD 'nin ikizkenar üçgeninde \angle ACD = \angle ADC yani;
$$ \angle ACD = \angle ADC = 70^\circ $$
Çünkü, üçgenin iç açıları toplamı her zaman 180°dir:
$$ 180^\circ - 40^\circ = 140^\circ $$
$$ 140^\circ \div 2 = 70^\circ $$
\angle ADC = 70^\circ tamamı \angle ADE= 70^\circ+120^\circ = 190^\circ
Bu verilenlere yenilerini eklyerek çözüm olan adımlara geçilebilir
$$ \angle ADB= 190° -:
( D, C bir farklı BC üzerinde üçgen olarak tez edilen
sonuç adımlarında kombinasyonların içerilerine bakılarak
X açısının:$:
adde:
### Sonuç olarak x açı: $\boxed{10^\circ}$ oluverdir.