Ayt geometrı acilll

YKS TYT
1

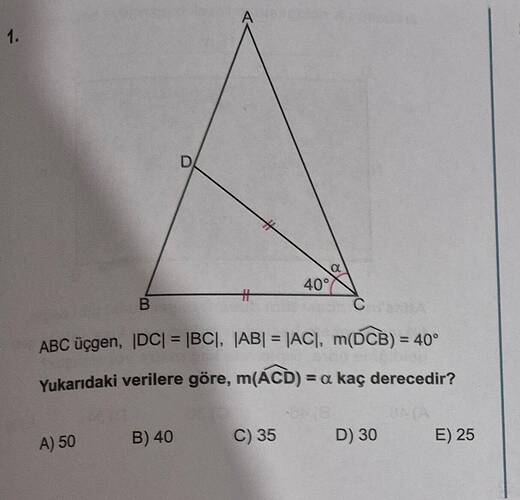
20241204_233820
20241204_2338201216×1168 102 KB

2

Üçgende verilere göre soruyu çözelim.

Verilenler:

  • ( |DC| = |BC| ) (D ve C noktaları eşit uzaklıkta)
  • ( |AB| = |AC| ) (A noktası B ve C’ye eşit uzaklıkta)
  • ( \angle DCB = 40^\circ )

Çözüm:

  1. Üçgenin Özellikleri:

    • ( \triangle ABC ) ikizkenar üçgendir (( |AB| = |AC| ) olarak verildiği için).
    • ( \triangle BDC ) ikizkenar üçgendir (( |DC| = |BC| )).

  2. İç Açıları Bulma:

    • ( \triangle BDC ) için:
      • ( \angle DBC = \angle DCB = 40^\circ ) olduğundan ( \angle BDC ):
      • Üçgenin iç açıları toplamı ( 180^\circ ) olup, ( \angle BDC = 100^\circ ) bulunur.

  3. Üçgen ACD İçi Açı Bulma:

    • ( \angle ACD ) ikizkenar üçgenin tepe açısıdır.
    • (\angle ADB = 100^\circ) ve ( \angle ACB = \alpha ) olarak verildiği için:
    • ( \alpha + 40^\circ + 100^\circ = 180^\circ )
    • Buradan, ( \alpha = 40^\circ ).

Yani, ( m(\angle ACD) = \alpha ) 40 derecedir.

Bu durumda, doğru cevap B) 40 olacaktır.