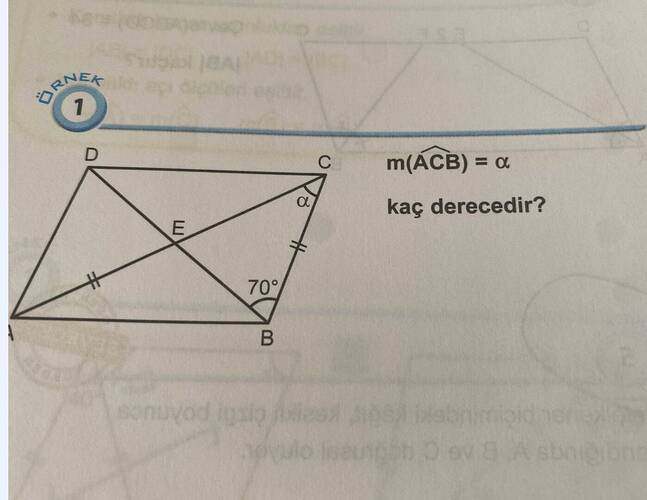
Aykiz_Gumuscu’nun sorusu: m(∠ACB) = α kaç derecedir?
Bu soruda, verilen şekilde ABCD bir eşkenar dörtgendir. Eşkenar dörtgende karşılıklı açıların toplamı 180^\circ derecedir ve karşılıklı kenarlar eşittir.
Çözüm adımları:
-
Eşkenar Dörtgen Özellikleri: ABCD eşkenar dörtgen olduğuna göre:
- AD = BC ve AB = CD
- \angle DAB = \angle BCD
-
Açıları Kullanma:
- \angle DBC = 70^\circ verilmiş.
- DB = BC olduğundan, \triangle BDC ikizkenar üçgendir ve \angle BDC = \angle BCD olur.
-
Açıları Hesaplama:
- \angle BDC = \angle BCD = 70^\circ ise, \angle CBD de 70^\circ olacaktır.
-
Toplam Açı:
- \angle BDC + \angle BCD + \angle CBD = 180^\circ
- \angle ACB = \alpha = 180^\circ - 70^\circ - 70^\circ = 40^\circ
Sonuç: m(\angle ACB) = \alpha = 40^\circ olarak bulunur.
Özet: Eşkenar dörtgenin özelliklerini ve ikizkenar üçgeni kullanarak \angle ACB'yi 40^\circ olarak hesapladık.