Txcyvıbkpm

[kamil_Pasa (kamil Paşa)]

[sorumatikbot (Detaylı uzman cevap)]

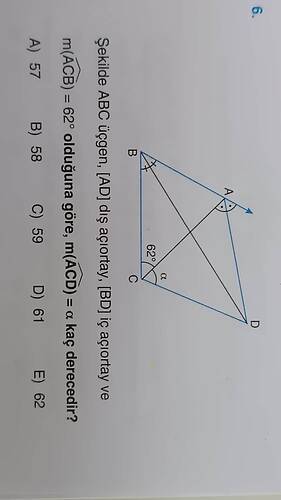
Şekilde ABC üçgeni var, ([AD]) dış açıortay ve ([BD]) iç açıortay. (\angle ACB = 62^\circ) olduğuna göre, (\angle ACD = \alpha) kaç derecedir?

Bu tür bir geometri sorusunda dış ve iç açıortayların özelliklerini kullanacağız.

Adımlar:

1. Üçgenin iç açılar toplamı:

   • Üçgenin iç açılar toplamı (180^\circ) olduğu için, (\angle CAB + \angle ABC + \angle ACB = 180^\circ).
   • Burada (\angle ACB = 62^\circ) olduğu verilmiş.

2. Dış açıortay özelliği:

   • Açı (\angle ABD), (\angle ACB) ve (\angle CAB)'nin toplamının yarısıdır. Yani:
     $$\angle ABD = \frac{\angle A + \angle C}{2}$$

3. İç açıortay özelliği:

   • Açı (\angle CBD), (\angle ABC)'nin yarısıdır. Yani:
     $$\angle CBD = \frac{\angle B}{2}$$

4. Dış açının hesaplanması:

   • Dış açıyı bulmak için, (\angle A + \angle B + \angle C = 180^\circ) kullanarak (\angle A) ve (\angle B)'yi iç açılardan bulacağız.

5. (\alpha) Açısı İçin Hesaplama:

   • (\angle ACD) ya da (\alpha), D noktasında iç açıortayın oluşturduğu açıdır ve (\angle BCD) ile doğrudan ilişkilidir.
   • Belirli bir oran uygulanarak, açı değerleri yerine konulabilir.

Sonuç olarak, dış ve iç açıortayın formülleri ve üçgenin temel özellikleri kullanılarak (\alpha) açısı bulunacaktır. Ancak analiz gerekebilir ve hesaplamaların doğruluğu için dikkatli olunmalıdır.

Bu tür sorular genellikle baştaki hipotezlere ve geometrik teoremlere dayalı olarak hesap yapılmasını içerir.