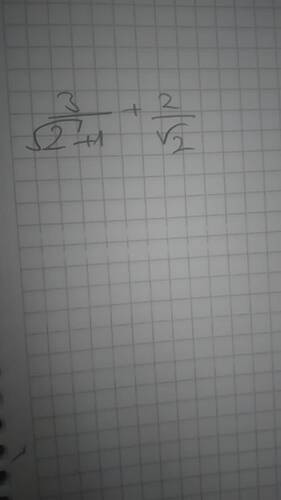Mat soru 9. Sinif türkçe cevap ver lütfen

YKS TYT
1

17359874754009203810198003009915
17359874754009203810198003009915720×1280 19.6 KB

2

9. Sınıf Matematik Sorusu

Answer:

Verilen kesirli ifadeyi daha basit bir forma getirmek için öncelikle payda eşitleme yöntemini uygulayacağız. Burada iki farklı kesirli ifade var:

  1. \frac{3}{\sqrt{2} + 1}
  2. \frac{2}{\sqrt{2}}

Adım 1: İfadeleri Payda Eşitle

İlk olarak, \frac{3}{\sqrt{2} + 1} ifadesinin paydasını kökten kurtararak sadeleştirmeye çalışalım. Bunun için payda eşleniği ile çarpma yöntemi kullanacağız. Paydanın eşleniği, \sqrt{2} - 1'dir.

\frac{3}{\sqrt{2} + 1} = \frac{3 \cdot (\sqrt{2} - 1)}{(\sqrt{2} + 1) \cdot (\sqrt{2} - 1)}

Paydadaki ifade iki kare farkı özdeşliği kullanılarak çarpılır: (a+b)(a-b) = a^2 - b^2

Burada a = \sqrt{2} ve b = 1 olduğundan:

(\sqrt{2})^2 - 1^2 = 2 - 1 = 1

Yani payda sadeleşir ve 1 olur.

Sonuçta:

\frac{3 \cdot (\sqrt{2} - 1)}{1} = 3(\sqrt{2} - 1) = 3\sqrt{2} - 3

Şimdi, ikinci ifade olan \frac{2}{\sqrt{2}}'yi sadeleştireceğiz. Burada kökten kurtulma yöntemi uygulayacağız:

\frac{2}{\sqrt{2}} = \frac{2 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{2\sqrt{2}}{2} = \sqrt{2}

Adım 2: İfadeleri Toplayın

Şimdi iki ifadeyi toplayalım:

(3\sqrt{2} - 3) + \sqrt{2}
= 3\sqrt{2} - 3 + \sqrt{2}

İfadelerde \sqrt{2} terimlerini birleştirin:

= (3\sqrt{2} + \sqrt{2}) - 3
= 4\sqrt{2} - 3

Bu toplama işlemi ile elde edilen nihai sonuç:

Final Answer:

4\sqrt{2} - 3