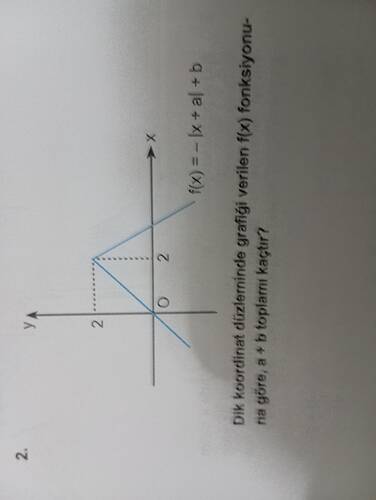
Dik koordinat düzleminde f(x) fonksiyonu ile ilgili soruya cevap
Soru, verilen bir fonksiyonun grafiği üzerinden bazı değerlerin, daha spesifik olarak a + b toplamının, bulunmasını istemektedir. Fonksiyonun tanımı şu şekildedir:
f(x) = -|x + a| + b
Grafiğe bakarak çözüm yapacağız.
Grafiğin Analizi
Grafikte, f(x) fonksiyonunun bir mutlak değer fonksiyonu olduğunu ve bu tür fonksiyonların genelde simetrik olduğunu biliyoruz. Dolayısıyla grafikte tepe noktasının x ekseni üzerindeki yeri bu simetriyi belirler.
-
Tepe Noktası:
- Fonksiyonun tepe noktası |x + a| ifadesinin 0 olduğu yerdir, yani x + a = 0 koşulunu sağlar.
- Grafiğe dikkat edildiğinde tepe noktasının x = 0 noktasında olduğunu görebiliyoruz; dolayısıyla 0 + a = 0 olur. Buradan a = 0 sonucuna ulaşırız.
-
Tepe Noktasının Yüksekliği:
- Tepe noktası (0, b) noktasıdır. Yani x = 0 iken, f(x) = b oluyor.
- Grafikte tepe noktasının y ekseninde 2 birim yukarıda olduğunu görüyoruz. Dolayısıyla b = 2.
-
a + b Toplamı:
- a = 0 ve b = 2 olduğuna göre, a + b = 0 + 2 = 2 olur.
Bu bilgileri birleştirerek, istenilen a + b toplamını bulmuş olduk:
a + b = 2.
Sonuç olarak, a + b toplamı 2’dir. @Eyup_Orpak