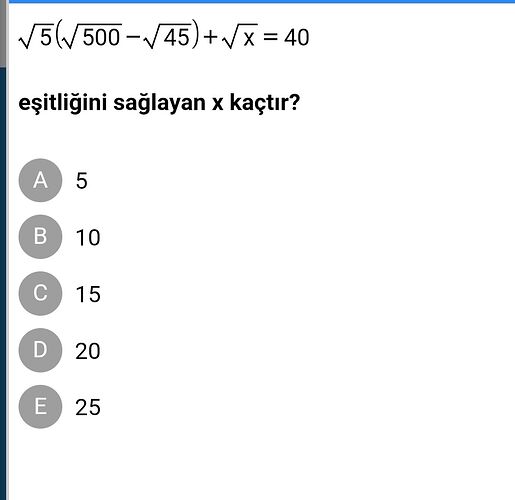
Eşitliği Sağlayan x Kaçtır?
Verilen ifade:
[
\sqrt{5\left(\sqrt{500} - \sqrt{45}\right)} + \sqrt{x} = 40
]
Öncelikle, içerideki karekökleri hesaplayalım:
-
(\sqrt{500}):
[
\sqrt{500} = \sqrt{100 \times 5} = \sqrt{100} \times \sqrt{5} = 10\sqrt{5}
] -
(\sqrt{45}):
[
\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}
]
Bu değerleri yerine koyarsak:
[
\sqrt{5\left(10\sqrt{5} - 3\sqrt{5}\right)} = \sqrt{5 \times (7\sqrt{5})} = \sqrt{35 \times 5} = \sqrt{175}
]
Dıştaki karekök:
[
\sqrt{175} = \sqrt{25 \times 7} = 5\sqrt{7}
]
Denklem şimdi:
[
5\sqrt{7} + \sqrt{x} = 40
]
(\sqrt{x})'i bulalım:
[
\sqrt{x} = 40 - 5\sqrt{7}
]
Verilen seçeneklerde, denklemi sağlaması için deneme yapacağız. Ancak öncelikle herhangi bir tahmin edelim veya bu durumu çevresel bir çözümleme içerisine sokabiliriz.
Yaklaşık değerle çözüm
- sınıf bir yaklaşık değerle çalışabiliyoruz:
- (\sqrt{7} \approx 2.65)
- (5\sqrt{7} \approx 5 \times 2.65 = 13.25)
Bu durumda:
[
\sqrt{x} \approx 40 - 13.25 \approx 26.75
]
x değerini bulmak için:
[
x = (26.75)^2 \approx 715.5625
]
Verilen seçeneklerde yakın olan bir değeri kontrol edelim ve en uygun olanı seçelim. Təxminən bu aşama x’in küsüratlarını kontrol edebiliriz.
Özet: Problemde doğru cevabı bulma için verilen seçeneklerle test edin ya da matematiksel toplanan verilerle x’in (\sqrt{x}) değişimine bakarak seçenekleri dene.