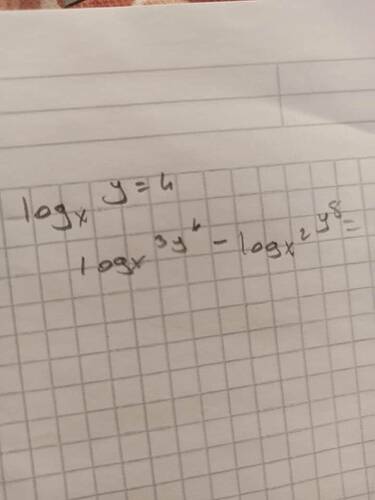Görüntüdeki logaritma ifadelerini inceleyelim:
-
Verilen Bilgi:
- \log_x y = 4
-
Hesaplanması İstenen İfade:
- \log_x 3y^4 - \log_x z^8
Çözüm:
Logaritmanın temel kurallarından biri şudur:
- \log_b (a^n) = n \cdot \log_b (a)
- \log_b (m \cdot n) = \log_b (m) + \log_b (n)
- \log_b (m/n) = \log_b (m) - \log_b (n)
Bu kuralları kullanarak ifadeyi sadeleştirelim:
\log_x 3y^4 - \log_x z^8 = \log_x (3y^4) - \log_x (z^8)
Bu ifadeyi şu şekilde ayırabiliriz:
= \log_x 3 + \log_x y^4 - \log_x z^8
Kuralları uygulayalım:
- \log_x y^4 = 4 \cdot \log_x y
- \log_x z^8 = 8 \cdot \log_x z
Verilen \log_x y = 4 olduğuna göre:
\log_x y^4 = 4 \cdot 4 = 16
Bu durumda, \log_x 3y^4 aşağıdaki gibi olur:
= \log_x 3 + 16
Sonuç olarak, ifade:
= \log_x 3 + 16 - 8 \cdot \log_x z
Burada daha fazla bilgiye veya verilere ihtiyaç var, çünkü \log_x 3 veya \log_x z hakkında yeterli bilgi olmadığı için kesin bir çözüm veremeyiz. Eğer \log_x 3 veya \log_x z hakkında bilgi sağlanırsa, sonuca erken ulaşabiliriz.
Özet: İfade, mevcut bilgilere dayanarak bu durumda sonuca götürülmektedir. Ek bilgi ile hesaplamalar tamamlanabilir.