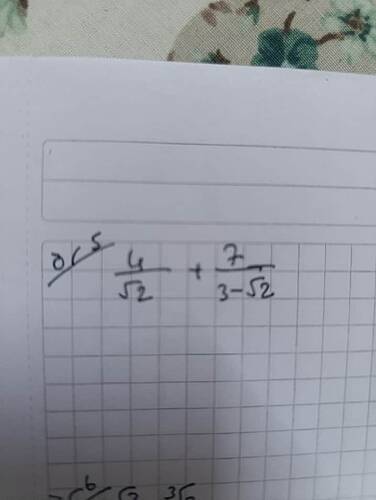Görüntüdeki matematik ifadesini anlamaya çalışalım.
İfade şu şekildedir:
$$\frac{4}{\sqrt{2}} + \frac{7}{3 - \sqrt{2}}$$
Bu denklemi nasıl çözeriz?
Adım 1: İlk Kesiri Düzenleme
İlk kesirdeki köklü ifadeyi düzenlemek için paydayı rasyonel hale getirebiliriz:
$$\frac{4}{\sqrt{2}} = \frac{4 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{4\sqrt{2}}{2} = 2\sqrt{2}$$
Adım 2: İkinci Kesirin Paydasını Rasyonel Hale Getirme
İkinci kesirdeki paydanın kökten kurtulmak için payda ile payı eşlenikle çarpmalıyız:
Eşlenik: 3 + \sqrt{2}
Bu, kesiri şu hale getirir:
$$\frac{7}{3 - \sqrt{2}} \cdot \frac{3 + \sqrt{2}}{3 + \sqrt{2}} = \frac{7(3 + \sqrt{2})}{(3 - \sqrt{2})(3 + \sqrt{2})}$$
Payda çarpımı:
$$(3 - \sqrt{2})(3 + \sqrt{2}) = 3^2 - (\sqrt{2})^2 = 9 - 2 = 7$$
Dolayısıyla:
$$\frac{7(3 + \sqrt{2})}{7} = 3 + \sqrt{2}$$
Adım 3: Kısımları Birleştirme
Şimdi her iki ifadeyi toplarız:
$$2\sqrt{2} + 3 + \sqrt{2} = 3 + 3\sqrt{2}$$
Sonuç olarak ifademiz 3 + 3\sqrt{2} olur.
Bu adımlarla köklü sayılarla işlemi tamamladık. İfadenin sadeleştirilmesi ve rasyonelleştirilmesi ile çözüme ulaştık.