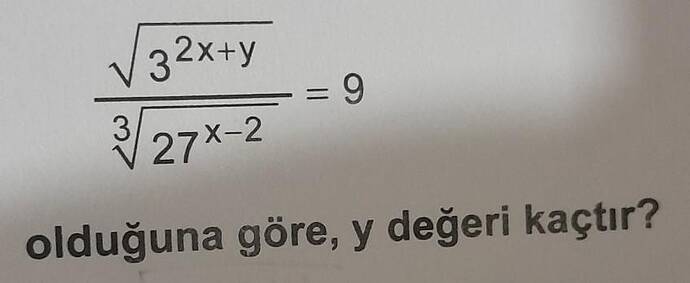Verilen İfade:
[ \frac{\sqrt[3]{3^{2x+y}}}{\sqrt[3]{27^{x-2}}} = 9 ]
Çözüm:
Önce, ifadeleri kökten kurtaralım. Küp kök, üssü \frac{1}{3} almak anlamına gelir, yani:
[ (3^{2x+y})^{\frac{1}{3}} = 3^{\frac{2x+y}{3}} ]
[ (27^{x-2})^{\frac{1}{3}} = 27^{\frac{x-2}{3}} ]
27 sayısı, 3^3 olarak yazılabilir, bu yüzden:
[ 27^{\frac{x-2}{3}} = (3^3)^{\frac{x-2}{3}} = 3^{x-2} ]
Bu durumda:
[ \frac{3^{\frac{2x+y}{3}}}{3^{x-2}} = 9 ]
9 sayısı, 3^2 olarak yazılabilir, bu sebeple:
[ 3^{\frac{2x+y}{3} - (x-2)} = 3^2 ]
Üsleri eşitleyelim:
[ \frac{2x+y}{3} - (x-2) = 2 ]
Parantezi açarak ve benzer terimleri birleştirerek:
[ \frac{2x+y}{3} - x + 2 = 2 ]
Bu denklemi çözmek için tüm terimleri eşitliğin bir tarafına toplarız:
[ \frac{2x + y}{3} - x + 2 = 2 ]
[ \frac{2x + y}{3} - x = 0 ]
Her iki tarafı 3 ile çarparız:
[ 2x + y - 3x = 0 ]
Bu ifadeyi sadeleştirirsek:
[ -x + y = 0 ]
Buradan:
[ y = x ]
Sonuç:
[ y ] değeri ( x ) ile eşittir. Kısaca, ( y = x ) olacaktır.