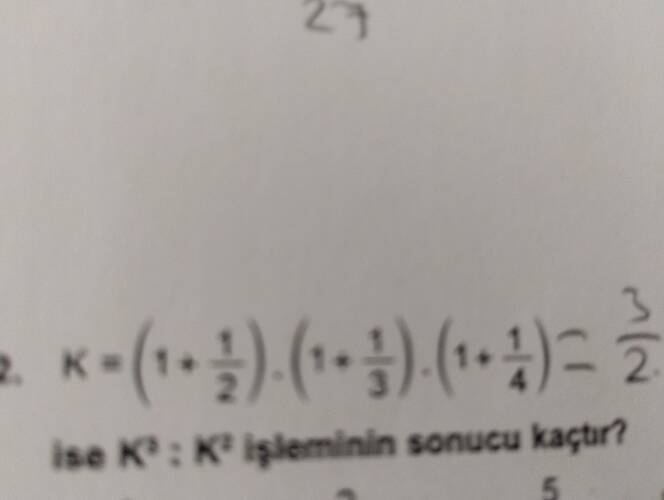Verilen ifadede K, aşağıdaki gibi tanımlanmıştır:
K = \left(1 + \frac{1}{2}\right) \cdot \left(1 + \frac{1}{3}\right) \cdot \left(1 + \frac{1}{4}\right)
Bu ifade hesaplanacak ve ardından K^3 : K^2 işlemi yapılacaktır.
Adım 1: K değerini hesaplayalım
İlk olarak, her bir parantez içindeki ifadeyi hesaplamamız gerekiyor:
- \left(1 + \frac{1}{2}\right) = \frac{3}{2}
- \left(1 + \frac{1}{3}\right) = \frac{4}{3}
- \left(1 + \frac{1}{4}\right) = \frac{5}{4}
Şimdi bu değerlerin çarpımını bulalım:
K = \frac{3}{2} \cdot \frac{4}{3} \cdot \frac{5}{4}
Çarpma işlemini adım adım yapalım:
-
İlk olarak \frac{3}{2} ve \frac{4}{3}'ü çarpalım:
\frac{3}{2} \cdot \frac{4}{3} = \frac{12}{6} = 2 -
Şimdi elde edilen sonucu \frac{5}{4} ile çarpalım:
2 \cdot \frac{5}{4} = \frac{10}{4} = \frac{5}{2}
Böylece, K = \frac{5}{2} bulunmuştur.
Adım 2: K^3 : K^2 Hesaplaması
Şimdi K^3 ve K^2'yi bulalım ve bölme işlemini yapalım:
- K^3 = \left(\frac{5}{2}\right)^3 = \frac{125}{8}
- K^2 = \left(\frac{5}{2}\right)^2 = \frac{25}{4}
K^3 değerini K^2 değerine bölelim:
\frac{K^3}{K^2} = \frac{\frac{125}{8}}{\frac{25}{4}}
Bu kesirler ile bölme işlemi yaparken ikinci kesiri ters çevirip çarparız:
\frac{125}{8} \cdot \frac{4}{25} = \frac{500}{200} = \frac{5}{2}
Sonuç olarak, K^3 : K^2 işleminin sonucu \frac{5}{2}'dir.