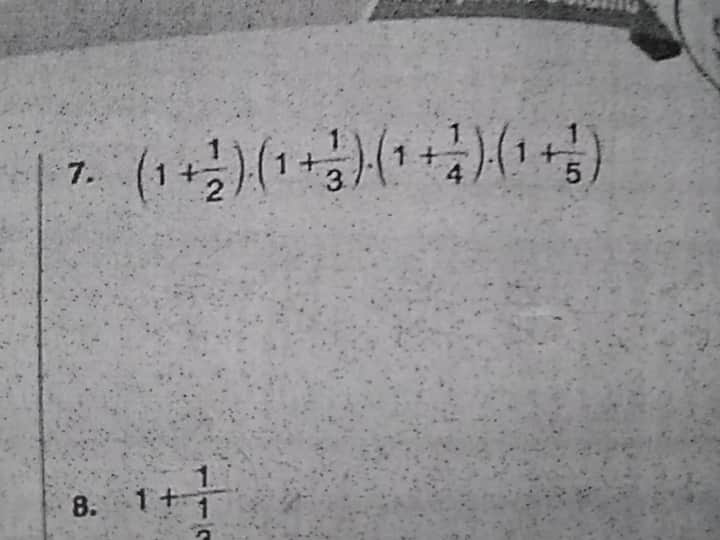Verilen ifadeyi hesaplayın: \left( 1 + \frac{1}{2} \right) \left( 1 + \frac{1}{3} \right) \left( 1 + \frac{1}{4} \right) \left( 1 + \frac{1}{5} \right)
Cevap:
İfadeyi parantez içlerini ayrı ayrı hesaplayarak ilerleyelim:
-
1 + \frac{1}{2}:
$
1 + \frac{1}{2} = \frac{2}{2} + \frac{1}{2} = \frac{3}{2}
$ -
1 + \frac{1}{3}:
$
1 + \frac{1}{3} = \frac{3}{3} + \frac{1}{3} = \frac{4}{3}
$ -
1 + \frac{1}{4}:
$
1 + \frac{1}{4} = \frac{4}{4} + \frac{1}{4} = \frac{5}{4}
$ -
1 + \frac{1}{5}:
$
1 + \frac{1}{5} = \frac{5}{5} + \frac{1}{5} = \frac{6}{5}
$
Bu oranları çarpacak olursak:
$
\left(\frac{3}{2}\right) \left(\frac{4}{3}\right) \left(\frac{5}{4}\right) \left(\frac{6}{5}\right)
$
Çarpma İşlemi:
Ortak terimler bölündüğünde, bu çarpma işlemi oldukça basitleşir:
$
= \frac{3}{2} \times \frac{4}{3} \times \frac{5}{4} \times \frac{6}{5}
$
$
= \frac{3 \times 4 \times 5 \times 6}{2 \times 3 \times 4 \times 5}
$
Buradaki ortak faktörler sadeleşecektir:
- 3, 4 ve 5’ler sadeleşir:
$
= \frac{6}{2} = 3
$
Bu hesaplama sonucunda, ifade 3’e eşittir.