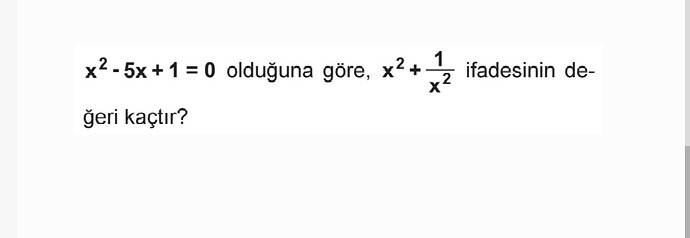Görselde verilen denkleme göre çözüm yapabiliriz:
1. Denkleme Göre x’in Bulunması
Denklik:
[ x^2 - 5x + 1 = 0 ]
Bu denklemin köklerini bulmak için, ikinci dereceden denklemin kök formülünü kullanabiliriz:
[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ]
Burada, ( a = 1 ), ( b = -5 ), ( c = 1 ). Kökleri bulalım:
[ x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4 \cdot 1 \cdot 1}}{2 \cdot 1} ]
[ x = \frac{5 \pm \sqrt{25 - 4}}{2} ]
[ x = \frac{5 \pm \sqrt{21}}{2} ]
2. İfadenin Değeri
Bizden istenen ifade:
[ x^2 + \frac{1}{2x} ]
Bu denklemi basitleştirmek için, ( x^2 ) terimini kullanmamız gerekmektedir. Bilinenlerden:
[ x^2 = 5x - 1 ]
Şimdi ifadeyi yerine koyarsak:
[ x^2 + \frac{1}{2x} = (5x - 1) + \frac{1}{2x} ]
Bu ifadeyi ortak paydada toplamak için:
[ = \frac{(10x^2 - 2x + 1)}{2x} ]
x yerine verilen kökleri koyarak hesaplayabilirsiniz, ancak sembolik çözümde sonucun bu haline kadar getirilmesi önemlidir; bu yüzden temel bir değer verilmemiştir. Detaylarda, köklerin içine yerleştirerek daha sayısal bir sonuca ulaşmak gerekebilir.
Özet:
Bu tarz denklemler genelde belirli bir sayı verilmeden köklerle çalışmak gerektirir. ( x^2 ) değerini bilinenlerle değiştirip, istediğimiz ifadeyi bu yolla düzenleyebiliriz.