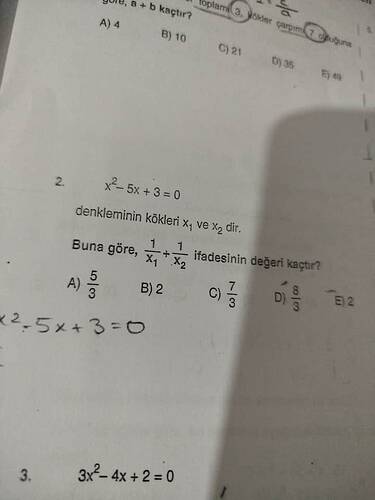( x^2 - 5x + 3 = 0 ) denkleminin kökleri ( x_1 ) ve ( x_2 ) olduğuna göre, ( \frac{1}{x_1} + \frac{1}{x_2} ) ifadesinin değeri kaçtır?
Cevap:
Verilen denklemde, ( x_1 ) ve ( x_2 ) kökleridir. ( \frac{1}{x_1} + \frac{1}{x_2} ) toplamını bulmak için şu formülü kullanacağız:
\frac{1}{x_1} + \frac{1}{x_2} = \frac{x_1 + x_2}{x_1 \cdot x_2}
1. Köklerin Toplamı ve Çarpımı:
İkinci dereceden denklemler için köklerin toplamı ve çarpımı şöyle bulunur:
- Köklerin toplamı: ( x_1 + x_2 = -\frac{b}{a} = -\frac{-5}{1} = 5 )
- Köklerin çarpımı: ( x_1 \cdot x_2 = \frac{c}{a} = \frac{3}{1} = 3 )
2. Verilen İfade Hesaplama:
Verilen ifadenin sonuç değeri:
\frac{1}{x_1} + \frac{1}{x_2} = \frac{x_1 + x_2}{x_1 \cdot x_2} = \frac{5}{3}
Bu durumda, doğru yanıt (\frac{5}{3}) olup seçenek A’dır.