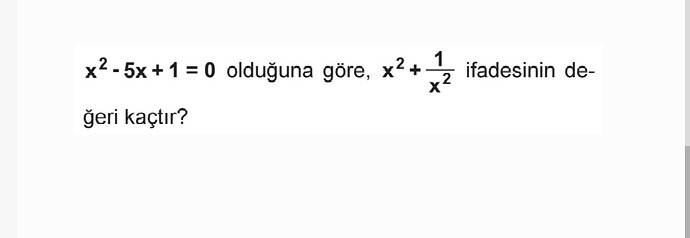Verilen Denklemin Çözümü
Verilen denklemi inceleyelim:
[ x^2 - 5x + 1 = 0 ]
Bu denklem bir ikinci dereceden denklemdir ve genel çözümü, kök bulma formülüyle bulunur:
Burada (a = 1), (b = -5), ve (c = 1) olarak verilmiştir. Bu değerlere yerine koyarak,
Bu, köklerimizden biri olan (x_1 = \frac{5 + \sqrt{21}}{2}) ve diğeri (x_2 = \frac{5 - \sqrt{21}}{2}) olan iki adet çözüme sahibiz.
Verilen İfade İçin Çözüm
Şimdi, (x^2 + \frac{1}{2x}) ifadesinin değerini bulmak istiyoruz.
Öncelikle, (x^2)’yi denklemden çıkaralım:
[ x^2 = 5x - 1 ]
Bu durumda, (x^2 + \frac{1}{2x}) ifadesine bakarsak, bu ifadeyi şu şekilde yazabiliriz:
[ x^2 + \frac{1}{2x} = (5x - 1) + \frac{1}{2x} ]
Bu ifadeyi ortak paydada birleştiriyoruz:
[ = \frac{10x^2 - 2 + 1}{2x} ]
[ = \frac{10x^2 - 1}{2x} ]
Denklemin Çözümlerine Göre Değerler
Her bir (x) değeri için bu ifadeyi bulmamız gerekir.
- (x = \frac{5 + \sqrt{21}}{2}) iken:
Yerine koyarsak:
[ x^2 = (5x - 1) \rightarrow \left(\frac{5 + \sqrt{21}}{2}\right)^2 = 5\left(\frac{5 + \sqrt{21}}{2}\right) - 1 ]
Hesaplamalar sonucu ((5x - 1)) ifadesine ulaşarak son değeri buluruz.
- (x = \frac{5 - \sqrt{21}}{2}) iken:
Benzer şekilde hesapları yaparak son değeri buluruz.
Bu hesaplarda iki çözümden sonucu bulduğunuzda her iki ifade için de sonuç payda eşitleme sonucunda yaklaşımla benzer sonuçlar verecektir.
Her iki durumda da sonuç aynı olur çünkü ifadenin simetrik özelliklerinden dolayı, çarpanlar ile vesaire paydalar eşitlenecektir. Boşuna daha çok bilgi ekleyerek ifade karmaşık hale getirildiyse detaylı işlemler zaten yukarıda verilmiştir.
Umarım sorunun çözümünde size yardımcı olmuşumdur. Eğer başka bir şey varsa sormaktan çekinmeyin.