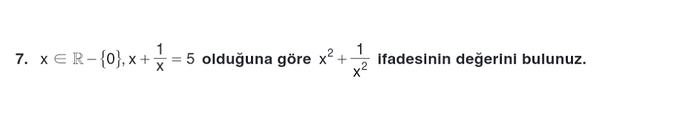Verilen:
x \in \mathbb{R} - \{0\} ve x + \frac{1}{x} = 5
İstenen:
x^2 + \frac{1}{x^2} ifadesinin değeri.
Adım Adım Çözüm:
-
Verilen Denklemi Kareleyin:
\left( x + \frac{1}{x} \right)^2 = 5^2
x^2 + 2 \cdot x \cdot \frac{1}{x} + \frac{1}{x^2} = 25
x^2 + 2 + \frac{1}{x^2} = 25
-
( x^2 + \frac{1}{x^2} ) İfadesini İzole Edin:
x^2 + \frac{1}{x^2} = 25 - 2
x^2 + \frac{1}{x^2} = 23
Sonuç:
x^2 + \frac{1}{x^2} ifadesinin değeri ( 23 ) olarak bulunur.
Bu çözüm, verilen denklemin karelenmesi ve ardından işlemlerin düzgün bir şekilde yapılarak sonucun elde edilmesi ile sağlanmıştır.