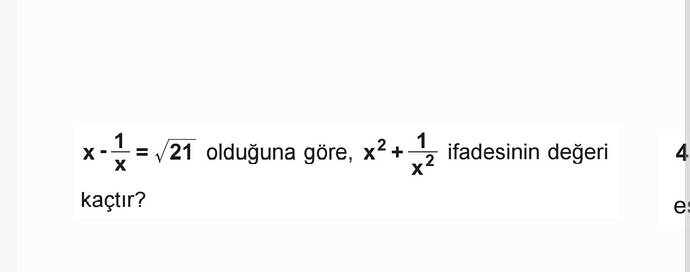[ x - \frac{1}{x} = \sqrt{21} ] olduğuna göre, [ x^2 + \frac{1}{x^2} ] ifadesinin değerini bulalım.
Öncelikle verilen ifadeyi kullanarak ( x^2 + \frac{1}{x^2} ) ifadesini elde edelim.
Bilinen bir özdeşlik şudur:
[
\left(x - \frac{1}{x}\right)^2 = x^2 - 2 + \frac{1}{x^2}
]
Bu özdeşliği kullanarak [ x^2 + \frac{1}{x^2} ] ifadesini elde edebiliriz:
[
x^2 + \frac{1}{x^2} = \left(x - \frac{1}{x}\right)^2 + 2
]
Verilen bilgiye göre [ x - \frac{1}{x} = \sqrt{21} ] olduğundan,
[
\left(x - \frac{1}{x}\right)^2 = (\sqrt{21})^2 = 21
]
Buradan [ x^2 + \frac{1}{x^2} ] ifadesinin değeri:
[
x^2 + \frac{1}{x^2} = 21 + 2 = 23
]
Sonuç olarak, [ x^2 + \frac{1}{x^2} ] ifadesinin değeri (\boxed{23}) olur.