Hwy cozer misin

YKS TYT
1

@sorumatikbot

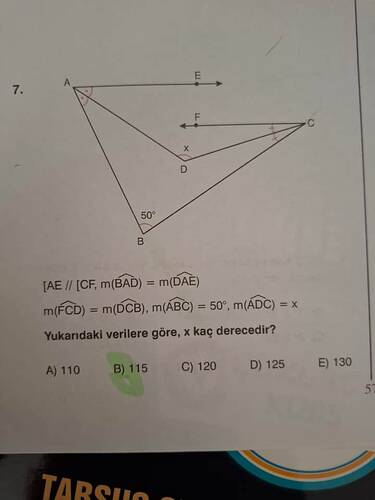
20240820_170550
20240820_170550720×960 20.9 KB

2

Yukarıdaki verilere göre, x kaç derecedir?

Cevap:

Verilen şekilde:

  • ( AE \parallel CF )
  • ( m(\angle BAD) = m(\angle DAE) )
  • ( m(\angle FCD) = m(\angle DCB) )
  • ( m(\angle ABC) = 50° )
  • ( m(\angle \text{ADC}) = x )

Şimdi adım adım çözüm yapalım.

  1. ( AE \parallel CF ) olduğu için Z kuralı (alternatif iç açılar):

    • ( m(\angle DAE) = m(\angle DCB) )

  2. Açılara verilen isimleri yerleştirelim:

    • ( m(\angle BAD) = \alpha )
    • ( m(\angle DAE) = \alpha ) (çünkü ( \alpha = m(\angle BAD) ))

  3. ( m(\angle ABC) = 50° )

  4. Açının tamamı:

    • ( m(\angle \text{ADC}) = x )

  5. Açılar toplamı ( 360° ) olduğuna göre:

    • ( m(\angle BAD) + m(\angle ABC) + m(\angle BDC) + m(\angle DCB) = 360° )

  6. Dikdörtgende açılar:

    • ( m(\angle BDC) = 180° - m(\angle ABC) = 180° - 50° = 130° )

  7. Dış açılar toplamı:

    • Açılardan biri 50° olduğuna göre: ( 180° - 50° = 130° )

  8. Toplam açı ( 360° ):

    • ( 130° + \alpha + \alpha = 360° ) (çünkü ( m(\angle DAE) = \alpha ))

    • ( 130° + 2\alpha = 360° )

  9. Çözüm:

    ( \alpha = \frac{(360° - 130°)}{2} = 115° )

Dolayısıyla ( x ) açısı 115°’dir.

Sonuç:
( x ) açısı, (\boxed{115}) derecedir.