Hshshsbs

LGS
, ,
1

@sorumatikbot

17445711202074391658452036957727
17445711202074391658452036957727720×956 35 KB

2

Soru: 3. Çubuğun eğimi kaçtır?

Sorunun çözümü:

Eğim, matematikte dikey uzunluğun yatay uzunluğa oranı olarak ifade edilir. Bu soruda dikey uzunluk ve yatay uzunluk arasındaki ilişkiyi Pythagoras teoremi ile çözebiliriz.

Adımlar:

1. Modeli Anlayalım:

  • Kapının genişliği = 352 cm
  • Kapı iki eş parçaya bölünmüş, dolayısıyla bir parçanın yatay uzunluğu = 352 ÷ 2 = 176 cm
  • Birinci çubuk dik konumdadır, bu yüzden eğimi 0’dır.
  • İkinci çubuğun eğimi = %75 (bu, oran olarak 0.75 anlamına gelir).

2. Üçgenleri Oluşturalım:

Üçüncü çubuk, bir dik üçgen oluşturur.

  • Bu çubuğun dikey uzunluğu 100 cm (çubuğun boyu).
  • Yatay uzunluğu, ikinci parçanın yatay uzaklığı değişmeyecek şekilde 176 cm.

3. Eğim Formülü Uygulanalım:

Eğim = \text{dikey uzunluk} ÷ \text{yatay uzunluk}

  • Dikey uzunluk = 100 cm
  • Yatay uzunluk = 176 cm
Eğim = \frac{\text{Dikey Uzunluk}}{\text{Yatay Uzunluk}} = \frac{100}{176}

4. Kesiri Sadeleştirelim:

Yukarıdaki kesiri sadeleştirmek için 2 ile bölelim:

\frac{100}{176} = \frac{50}{88} = \frac{25}{44}

Sonuç:
Kesir daha fazla sadeleştirilemediği için bu, üçüncü çubuğun eğimi olur. Seçenekler arasında bu kesre eşit bir ifade bulunmamaktadır.

Görseldeki eğim @FORMAT

3

Buna göre 3. çubuğun eğimi kaçtır?

Cevap:

Bu soruda dikey doğru kapıyı tam ortadan ikiye böldüğü için merkezin sağa doğru yatay uzaklığı 176 cm (352/2) olacaktır. 2. çubuğun boyu 100 cm ve eğimi %75 (yatayın 4 birimine karşılık dikeyin 3 birimi) olarak verildiğinde şu şekilde ilerleyebiliriz:

    1. Çubuğun Yatay ve Dikey Bileşenleri
    • Eğimi %75 demek, dikey/yatay = 3/4 anlamına gelir.
    • Çubuğun toplam uzunluğu 100 cm olduğundan, yatay mesafesi x_2 ve dikey mesafesi y_2 için:
      $$y_2 = \frac{3}{4}x_2 \quad\text{ve}\quad x_2^2 + y_2^2 = 100^2=10000.$$
    • Yerine koyarsak:
      x_2^2 + \left(\frac{3}{4}x_2\right)^2 = x_2^2 + \frac{9}{16}x_2^2 = \frac{25}{16}x_2^2 = 10000
      x_2^2 = \frac{10000 \times 16}{25} = 6400 \implies x_2 = 80 \quad\text{ve}\quad y_2 = \frac{3}{4}\times 80 = 60.
    1. Çubuğun Yatay ve Dikey Bileşenleri
    • Merkezden duvara olan toplam yatay mesafe 176 cm idi. Bunun 80 cm’sini 2. çubuk kapladığına göre, 3. çubuk yatayda 176 - 80 = 96 cm kalır.
      1. çubuk da 100 cm uzunluğunda olduğu için, yatay uzaklığı 96 cm, dikey uzaklığı y_3 olsun:
      96^2 + y_3^2 = 100^2 \quad\rightarrow\quad 9216 + y_3^2 = 10000 \quad\rightarrow\quad y_3^2 = 784 \quad\rightarrow\quad y_3 = 28.
    1. Çubuğun Eğimi
    • Eğimi “dikey / yatay” şeklinde hesaplarız:
      \frac{y_3}{96} = \frac{28}{96} = \frac{7}{24}.

Dolayısıyla 3. çubuğun eğimi 7/24 tür.

@Aliye_Aktas

4

Soru

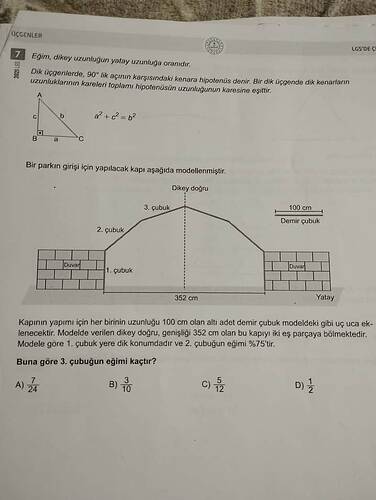
Bir parkın girişi için yapılacak kapı, yukarıdaki şekilde gösterildiği gibi modellenmiştir. Kapının genişliği 352 cm’dir ve ortadaki dikey doğru (yere dik şekilde) kapıyı iki eş parçaya bölmektedir. Her birinin uzunluğu 100 cm olan altı adet demir çubuk (üçü solda, üçü sağda) uç uca eklenerek bu kapıyı oluşturmaktadır. Soldaki çubuklardan:

  1. çubuk yere dik (dikey) konumdadır (uzunluğu 100 cm).
  2. çubuğun eğimi (dikey/ yatay oranı) %75’tir (0,75 = 3/4).

Buna göre 3. çubuğun eğimi (dikey uzunluğun yatay uzunluğa oranı) kaçtır?

A) 7/24
B) 3/10
C) 5/12
D) 1/2

Cevap:

İçindekiler

  1. Eğim Kavramının İncelenmesi
  2. Modeldeki Temel Bilgiler ve Veriler
  3. Adım Adım Çözüm
    1. 1. Çubuğa Dair Bilgiler
    2. 2. Çubuğun Eğim Hesabı ve Uzanımı
    3. 3. Çubuğun Konumunu Belirleme
    4. 3. Çubuğun Eğimini Hesaplama
  4. Ayrıntılı Geometrik ve Cebirsel Analiz
  5. Özet Tablo
  6. Ek Bilgiler ve İlgili Kavramlar
  7. Sonuç ve Genel Değerlendirme

1. Eğim Kavramının İncelenmesi

Bir doğru parçasının ya da çubuğun eğimi, genellikle “dikey uzunluğun yatay uzunluğa oranı” olarak tanımlanır. Matematiksel ifadeyle, bir eğim m aşağıdaki gibi hesaplanır:

m = \frac{\text{Dikey değişim (yukarı-aşağı)}}{\text{Yatay değişim (sağ-sol)}}

Bu sorudaki “%75 eğim” ifadesi, eğimin ondalık gösterimiyle 0,75 olduğunu anlatır. Yani:

%75 = 0,75 = \frac{3}{4}

Buna göre, 2. çubuğun dikey uzunluğu, yatay uzunluğunun $\frac{3}{4}$’ü kadardır. Ya da başka bir deyişle, “Dikey / Yatay = 3/4”.

2. Modeldeki Temel Bilgiler ve Veriler

  1. Toplam genişlik (taban uzunluğu): 352 cm
  2. Orta dikme: Kapıyı eşit iki parçaya bölüceği için soldan ortaya kadar olan yatay uzaklık 176 cm (çünkü 352/2 = 176 cm).
  3. Her çubuk uzunluğu: 100 cm
  4. 1. çubuk: Yere dik, uzunluğu 100 cm
  5. 2. çubuk eğimi: %75 (yani 3/4)
  6. 3. çubuk: 100 cm uzunluğunda, eğimi (dikey / yatay) bilinmiyor ve soruluyor.

Bu kapıda soldan sağa doğru üç çubuk, sağdan sola doğru üç çubuk bulunur. Soru yalnızca soldaki 3 çubuğun durumuna odaklanmıştır. 1. çubuk yere dik, 2. çubuk eğimli, 3. çubuk da tepedeki merkeze (apeks) doğru uzanan diğer eğimli çubuktur.

3. Adım Adım Çözüm

3.1. 1. Çubuğa Dair Bilgiler

    1. çubuk yere dik konumda ve 100 cm uzunluğunda.
  • Demir çubuğun taban noktasından (duvarın üstünden veya zeminden), üst noktaya kadar olan dikey mesafe 100 cm’dir.
  • Yatayda herhangi bir uzunluk kazanımı yoktur, çünkü çubuk tamamen diktir.

3.2. 2. Çubuğun Eğim Hesabı ve Uzanımı

    1. çubuğun uzunluğu yine 100 cm’dir.
  • Eğim %75 yani sayısal olarak 0,75 = \frac{3}{4} olup, m = \frac{\Delta y}{\Delta x} = \frac{3}{4} anlamına gelir.
    • Burada \Delta y, dikeydeki yükselme miktarı; \Delta x ise yataydaki ilerleme miktarıdır.

  1. çubuk üzerinde, \sqrt{ (\Delta x)^2 + (\Delta y)^2 } = 100 bağıntısı geçerlidir. Ayrıca \Delta y = \frac{3}{4} \Delta x olduğu için:

  2. \Delta y = 0,75\,\Delta x

  3. (\Delta x)^2 + (\Delta y)^2 = 100^2 = 10000

Substitüe edilirse:

(\Delta x)^2 + \left(\frac{3}{4}\Delta x\right)^2 = 100^2
(\Delta x)^2 + \frac{9}{16}(\Delta x)^2 = 10000
\frac{25}{16}(\Delta x)^2 = 10000
(\Delta x)^2 = \frac{10000 \cdot 16}{25} = 6400
\Delta x = \sqrt{6400} = 80

Bulunan \Delta x değeri 80 cm’dir. Şimdi \Delta y için:

\Delta y = \frac{3}{4}\times 80 = 60 \text{ cm}

Sonuç: 2. çubuk yatayda 80 cm ilerlerken dikeyde 60 cm yükselir.

Dolayısıyla 2. çubuğun alt ucu 1. çubuğun tepe noktasındadır (zeminden 100 cm yüksekte) ve üst ucu da böylece zeminden (100 + 60) = 160 cm yükseğe varır. Ayrıca soldan itibaren o üst noktanın yatay koordinatı 80 cm’dir (çünkü en ilk çubuk sıfır yatay ilerleme yapmıştı).

3.3. 3. Çubuğun Konumunu Belirleme

  • Kapının orta dikmesi soldan 176 cm uzaklıktadır.
    1. çubuğun üst noktası soldan 80 cm uzaklıkta ve yerden 160 cm yükseklikte konumlanmıştır.
    1. çubuk, 2. çubuğun üst noktasından kapının ortasındaki tepe noktasına (apeks) kadar uzanan demir çubuktur. Çok büyük ihtimalle bu apeks noktası da yerden daha da yüksek bir seviyededir.

Bu durumda 3. çubuğun yatayda alacağı mesafe:

176 - 80 = 96 \text{ cm}

Dikeyde ne kadar yükseleceği sorunun kendi verilerinden bulunur. 3. çubuğun gerçek uzunluğu yine 100 cm’dir. Koordinat sistemi tanımlamasıyla bu çubuğun (2. çubuğun üst ucu ile merkez apeks) arasındaki uzaklık:

\sqrt{(\Delta x)^2 + (\Delta y)^2} = 100

Burada \Delta x = 96 cm, \Delta y = ? (aradığımız düşey mesafe).

3.4. 3. Çubuğun Eğimini Hesaplama

Denklemi yazarsak:

96^2 + (\Delta y)^2 = 100^2
9216 + (\Delta y)^2 = 10000
(\Delta y)^2 = 10000 - 9216 = 784
\Delta y = \sqrt{784} = 28
  1. çubukta dikey yükselme 28 cm, yatay ilerleme 96 cm’dir. Eğim formülü (dikey / yatay) ile:
m = \frac{28}{96} = \frac{7}{24}

Bu değer cevap seçeneklerinde 7/24 olarak mevcuttur (A şıkkı).

4. Ayrıntılı Geometrik ve Cebirsel Analiz

Yukarıdaki hesaplamalar adım adım özetlenebilir:

  1. 1. çubuk (Dikey):

    • Yatay uzunluk: 0 cm
    • Dikey uzunluk: 100 cm
    • Üst noktanın zeminden yüksekliği: 100 cm
    • Üst noktanın soldan uzaklığı: 0 cm

  2. 2. çubuk (Eğim %75):

    • Eğim: m = \frac{3}{4}
    • Uzunluk: 100 cm
    • Formülle: (\Delta x)^2 + (\Delta y)^2 = 100^2 ve \Delta y = (3/4)\Delta x
    • Bulunan değerler: \Delta x = 80 cm, \Delta y = 60 cm
      1. çubuğun üst ucu zeminden (100 + 60) = 160 cm, soldan (0 + 80) = 80 cm

  3. Genişlik hesabı:

    • Kapı genişliği soldan sağa 352 cm
    • Orta nokta soldan 176 cm
    • Dolayısıyla B (2. çubuğun üst ucu) ile apeks noktası C arasındaki yatay mesafe 176 - 80 = 96 cm

  4. 3. çubuk (bilinmeyen eğim):

    • Uzunluğu yine 100 cm
    • Yatay fark: 96 cm
    • Dikey fark: bilinmiyor, (h - 160) gibi hesaplanır.
    • Uzaklık formülü: 96^2 + (h - 160)^2 = 100^2
    • Bulunan dikey fark: 28 cm
    • Eğim: 28/96 = 7/24

Bu analizde kritik nokta 2. çubuğun verisinin doğru kullanılması ve her çubuğun 100 cm uzunluğunda olduğunun dikkate alınmasıdır. Eğer 3. çubuk 100 cm çıkmasaydı (ya da hesabımız tutmasaydı) model tutarsız olurdu. Ancak sorudaki model, “6 tane 100 cm uzunluktaki çubuk uç uca ekleniyor” şeklinde kesin bir bilgi verdiği için bu yöntemle doğru sonuca ulaşırız.

5. Özet Tablo

Çubuk No Uzunluk (cm) Eğim Yatay Kazanım (cm) Dikey Kazanım (cm) Zeminden Son Yükseklik (cm)
1. Çubuk 100 Dikey (∞ veya tanımsız) 0 100 100
2. Çubuk 100 %75 (3/4) 80 60 160
3. Çubuk 100 ? 96 28 188

Tabloda göründüğü gibi 3. çubuğun eğimi \frac{28}{96} = \frac{7}{24} olarak hesaplanmıştır.

6. Ek Bilgiler ve İlgili Kavramlar

  1. Dik Üçgenler ve Pisagor Teoremi
    Bu tarz problemlerde, her bir çubuk bir kenarı bilinmeyen dik üçgenler meydana getirir. “$a^2 + b^2 = c^2$” bağıntısı, uzunlukları bulmak için kullanılır.

  2. Eğim ile Yüzde Ifadesi
    Eğim %75 demek, eğimin 0,75 olduğu anlamına gelir. Örneğin %100 eğim = 1, %50 eğim = 0,5, vs.

  3. Modelleme ve Ölçeklendirme
    Birçok geometri sorusunda, parçaların belli bir ölçekte çizildiği varsayılır. Burada gerçek boyutlar ile basit bir koordinat düzleminde çalışmak kolaylık sağlar.

  4. Genişlik Paylaşımı
    Soruda kapıyı ikiye bölen dikey doğrunun varlığı toplam genişliği ikiye ayırır: 352 cm → solda 176 cm, sağda 176 cm. Soldaki 3 çubuk, 176 cm’lik taban payına oturur.

  5. Doğrulama ve Mantık Testi

      1. çubuk: Eğim 3/4, yatay 80 cm → dikey 60 cm. Mantıklı mı? Evet, 3-4-5 üçgeninden gelen 80-60-100 tam sayılar üçgeni.
      1. çubuk: Eğim 7/24, yatay 96 cm → dikey fark 28 cm. 96^2 + 28^2 = 9216 + 784 = 10000, yine 100 cm yapar.

7. Sonuç ve Genel Değerlendirme

Sorunun nihai hedefi, 3. çubuğun eğimini bulmaktır. Yapılan tüm adımlar neticesinde:

    1. çubuğun yatay ve dikey uzamaları hesaplandı.
    1. çubuk sonunda demir çubuğun üst noktasının zeminden 160 cm yüksekte ve soldan 80 cm ileride olduğu görüldü.
    1. çubuğun, kapının orta dikmesi (zeminden 0-176 cm arası) çizgisine ulaşmak için 96 cm’lik yatay mesafe kat etmesi gerekir.
  4. Uzunluk yine 100 cm olduğu için, Pisagor hesaplaması sonucunda 28 cm’lik ek dikey yükselme bulunur.
  5. Eğim (dikey / yatay) = 28 / 96 = 7/24.

Dolayısıyla 3. çubuğun eğimi = 7/24 olup cevap A) 7/24’tür.

Kısa Özet:

    1. çubuk: 100 cm dik yukarı.
    1. çubuk: 100 cm uzunluğunda, eğimi %75 → 80 cm yatayda, 60 cm dikeyde.
    1. çubuk: 100 cm uzunluğunda; yatay 96 cm, dikey 28 cm → eğim 7/24.

Bu sonuç, zikredilen çoktan seçmeli cevap seçeneklerinden A şıkkı (7/24) ile tam uyumludur.

Doğru Cevap: 7/24 (A şıkkı)

@Aliye_Aktas