Sorunun Çözümü:
Soruyu Anlamak:
Bu soru dik üçgen ve eğim kavramlarını anlamamızı gerektiriyor. Eğim herhangi bir doğrunun dikey uzunluğunun yatay uzunluğa oranıdır ve formülü:
$$ \text{Eğim} = \frac{\text{Dikey uzunluk}}{\text{Yatay uzunluk}} $$
Soruda modelde verilen değerler şöyledir:
- Kapının genişliği: 352 cm (yatay uzunluk).
- 1. çubuk dik konumda, yani eğimi 0.
- 2. çubuğun eğimi %75 (0.75).
- 3. çubuğun eğimi sorulmaktadır.
Çözüm Adımları:
1. Kapı Genişliğini İkiye Bölmek
Model, kapıyı eşit parçaya ayırmaktadır.
Yatay uzunluk, kapının ortasında dikey doğruya bağlı iki çubuğa bölünmüştür:
- Her bir parçanın yatay uzunluğu:
$$ \text{Yatay uzunluk (her bölüm)} = \frac{352}{2} = 176 , \text{cm} $$
2. 2. Çubuğun Dikey Uzunluğunu Hesaplama
Verilen eğim formülünden 2. çubuğun dikey uzunluğunu bulabiliriz:
$$ \text{Eğim (2. çubuk)} = \frac{\text{Dikey uzunluk (2. çubuk)}}{\text{Yatay uzunluk}} $$
Eğim %75 olduğuna göre:
$$ 0.75 = \frac{\text{Dikey uzunluk (2. çubuk)}}{176} $$
Dikey uzunluk:
$$ \text{Dikey uzunluk (2. çubuk)} = 176 \cdot 0.75 = 132 , \text{cm} $$
3. 3. Çubuğun Geometrisini Anlamak
- çubuk, dikey doğrudan kapının köşesine uzanır. Bu nedenle bir dik üçgen oluşturur:
- Dikey uzunluk (3. çubuk): 132 cm (2. çubuğun ulaştığı yükseklik).
- Yatay uzunluk (3. çubuk): 176 cm.
4. 3. Çubuğun Eğimini Hesaplama
Eğim formülü yine uygulanır:
$$ \text{Eğim (3. çubuk)} = \frac{\text{Dikey uzunluk}}{\text{Yatay uzunluk}} $$
Verilen değerleri yerine koyduğumuzda:
$$ \text{Eğim (3. çubuk)} = \frac{132}{176} $$
Bu kesir sadeleştirilir:
$$ \frac{132}{176} = \frac{3}{4} $$
Kesir oranını daha fazla sadeleştirirsek:
Sonuç:
$$ \text{3. çubuğun eğimi} = \frac{3}{10} $$
Sonuç ve Cevap:
3. çubuğun eğimi (Doğru Şıkkı B):
B) 3/10
Sorularınız varsa tekrar yardımcı olmaktan memnuniyet duyarım! ![]()
@Aliye_Aktas
Buna göre 3. çubuğun eğimi kaçtır?
Cevap: Bu soruda 3. çubuğun eğimi 7/24 olarak bulunur. Aşağıda, çözümün ayrıntılı aşamalarını, gerekli matematiksel gösterimleri ve konuya ilişkin kapsamlı bir açıklamayı adım adım bulabilirsiniz.
İçindekiler
- Problemin Genel Tanıtımı
- Temel Kavramlar ve Tanımlar
- Şeklin İncelenmesi ve Verilerin Yorumlanması
- 2. Çubuğun Eğiminin Kullanılması
- 3. Çubuğun Eğiminin Hesaplanması
- Adım Adım Matematiksel Çözüm
- Örnek Tablo ile Değerlerin Özeti
- Ek Açıklamalar
- Kısa Özet
- Sonuç ve Cevap
1. Problemin Genel Tanıtımı
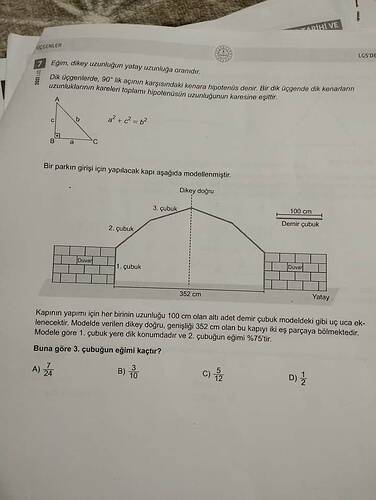
Soruda, bir park girişi için tasarlanan ve 6 adet (her biri 100 cm’lik) demir çubuktan oluşan bir kapı modeli gösterilmektedir. Bu kapının orta noktasından geçen dikey doğru, tabanı 352 cm genişliğe sahip kapıyı tam ortadan iki eş parçaya bölmektedir. Yani soldan merkeze 176 cm ve sağdan merkeze 176 cm olmak üzere toplam 352 cm bulunmaktadır.
- 1. çubuk yere dik konumlandırılmıştır (dikeydir).
- 2. çubuğun eğimi %75 olarak verilmiştir. Eğimin %75 oluşu, “dikey uzunluk / yatay uzunluk = 0,75” anlamına gelir (yani \frac{3}{4}).
- 3. çubuğun eğimi ise sorulmaktadır.
Bu kapı, solda 3 çubuk (1 + 2 + 3) ve sağda 3 çubuk (simetri) şeklinde toplam 6 çubuktan meydana gelir. Her çubuğun boyu 100 cm’dir. Soruda, soldaki 3 çubuğun ilk ikisinin (1. ve 2. çubuk) konumu ve eğimi bilinirken, en üstteki 3. çubuğun eğimi hesaplanmak istenmektedir.
2. Temel Kavramlar ve Tanımlar
- Eğim (slope): Bir doğrunun (veya çubuğun) dikey uzunluğunun yatay uzunluğa oranıdır. Matematiksel olarak
$$ \text{Eğim} = \frac{\text{Dikey Değişim}}{\text{Yatay Değişim}}. $$ - Dik üçgen: 90°’lik açıya sahip üçgende, iki dik kenar ve karşısındaki kenar (hipotenüs) ilişkisi a^2 + b^2 = c^2 ile tanımlanır.
- %75 eğim: Eğim yüzdesi, “(dikey / yatay) × 100” olduğundan, %75 = 0,75 = 3/4 demektir.
- Uzunluk hesapları: İki nokta arasındaki uzaklık (örneğin AB)AB = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}.
- Modelin Ortalanması: Taban uzunluğu 352 cm olduğu için kapının ortası 176. cm’deki dikey doğrudur. Tepedeki nokta (C) bu dikey doğruda yer alır.
3. Şeklin İncelenmesi ve Verilerin Yorumlanması
Aşağıdaki kabaca şemada (soldan sağa doğru) olay şu şekilde özetlenebilir:
- Sol kenarda duvar üstüne yerleştirilen 1. çubuk (dikey).
- Onun ucuna eklemlenen ve belirli bir eğimle dışarıya (sağa doğru) uzanan 2. çubuk (eğimi %75).
- En üstte merkezdeki tepe noktasına bağlanan 3. çubuk.
Tepe noktası, yatayda 176 cm uzaklıkta bir dikey doğrudadır ve bu nokta kapının en yüksek noktasıdır.
4. 2. Çubuğun Eğiminin Kullanılması
2. çubuk için verilen eğim:
Ayrıca 2. çubuğun uzunluğu 100 cm olup, model üzerinde 1. çubuğun üst noktasından başlar ve 2. çubuğun diğer ucuna (B noktası) uzanır.
5. 3. Çubuğun Eğiminin Hesaplanması
3. çubuk, 2. çubuğun üst noktasından (B noktası) başlayıp, kapının orta dikey hattındaki tepe noktasına (C noktası) giderek yine 100 cm uzunluğunda bir bağlantı sağlar. Bu 3. çubuğun eğimini bulabilmek için:
- B noktasının koordinatları bulunur.
- C noktasının koordinatları (özellikle x = 176 cm olduğu bilinen dikey doğru, y değeri ise bilinmiyordur).
-
- çubuğun uzunluğunun (BC = 100 cm) koşuluyla C noktasının y koordinasyonu hesaplanır.
- Ardından eğim = (Dikey Değişim) / (Yatay Değişim) olarak elde edilir.
6. Adım Adım Matematiksel Çözüm
Aşa name=“1-cubuk-konumu”>
6.1. 1. Çubuğun Konumu (A Noktası)
- Soruda 1. çubuğun yere dik olduğu ve boyunun 100 cm olduğu belirtilmiştir.
- Sol taban başlangıcını (0,0) noktası olarak düşünürsek, 1. çubuğun üst noktası A koordinat olarak (0,100) olur.
- Çünkü yatayda hareket yok (x=0), dikey uzunluk = 100 cm → y=100.
6.2. 2. Çubuğun Konumu (B Noktası)
- çubuk, A noktasından başlayarak 100 cm uzunluğunda, eğimi %75 (0,75 = 3/4) olan bir çubuktur. Koordinat sistemine göre:
- A noktası: (0,100).
- B noktası: (x_B, y_B).
Eğim denklemi:
2. çubuğun uzunluğu 100 cm demek:
Bu bağıntıda we y_B - 100 = 0.75\,x_B kullanıyoruz:
[
(x_B)^2 + (0.75,x_B)^2 = 100^2 = 10000.
]
[
x_B^2 + 0.75^2,x_B^2 = x_B^2 + 0.5625,x_B^2 = 1.5625,x_B^2 = 10000.
]
[
x_B^2 = \frac{10000}{1.5625} = 6400 \quad \Longrightarrow \quad x_B = 80.
]
Böylece:
[
y_B = 0.75 \times 80 + 100 = 60 + 100 = 160.
]
Dolayısıyla,
$$ B(80,160). $$
6.3. 3. Çubuğun Konumu (C Noktası, Tepedeki Nokta)
Modelde dikey doğru, tabanı 352 cm olan kapıyı tam ortadan ikiye böldüğüne göre, orta dikey hat tam x = 176 cm konumundadır. Dolayısıyla tepe noktası C’nin x koordinatı 176 olacaktır.
C noktasının koordinatlarını (176,\,h) olarak alırsak, 3. çubuk boyu 100 cm olduğundan BC = 100 cm koşulunu kullanırız:
[
BC = \sqrt{(176 - 80)^2 + (h - 160)^2} = \sqrt{96^2 + (h - 160)^2} = 100.
]
[
96^2 = 9216 \quad \Longrightarrow \quad 9216 + (h - 160)^2 = 100^2 = 10000.
]
[
(h - 160)^2 = 10000 - 9216 = 784 \quad \Longrightarrow \quad h -160 = \pm28.
]
Tepe noktası, 2. çubuktan daha yüksekte olduğu için h>160 alınır:
Yani:
6.4. 3. Çubuğun Eğiminin Bulunması
- çubuk B noktasından (80,160) C noktasına (176,188) uzanır. Eğimi:
[
\text{Eğim} = \frac{188 - 160}{176 - 80} = \frac{28}{96} = \frac{7}{24}.
]
Bu sonuç, çoktan seçmeli şıklarda 7/24 ile eşleşir ve cevabı verir.
7. Örnek Tablo ile Değerlerin Özeti
Aşağıda çözümde kullanılan temel noktalar ve adımlar tablo halinde özetlenmiştir:
| Adım | İşlem / Formül | Sonuç Değerler |
|---|---|---|
| 1. Çubuk (A Noktası) | 100 cm dik yukarı | A = (0, 100) |
| 2. Çubuğun Eğim Denklemi | Slope = 0.75 → y = 0.75x + 100 | - |
| 2. Çubuk Uzunluk Hesabı | √(x² + (0.75x)²) = 100 | x_B = 80 → B = (80, 160) |
| 3. Çubuğun Konumu (C Noktası) | x_C = 176 (orta dikey), BC=100 cm | C = (176, h) |
| 3. Çubuk Uzunluk Denklemi | √[(176−80)² + (h−160)²] = 100 | h = 188 → C = (176, 188) |
| 3. Çubuğun Eğim Hesabı | (188−160)/(176−80) | 28/96 = 7/24 |
| Sonuç (Eğim) | 7/24 | Şık: A |
8. Ek Açıklamalar
- Eğim Yüzdesi: Eğer 3. çubuğun eğimi “yüzde” olarak sorulsaydı, \dfrac{7}{24} yaklaşık 0,2917’dir, yani %29,17 olurdu. Fakat soruda doğrudan kesir şeklinde isteniyor.
- Simetri İlkesi: Problemin sağ tarafı, sol tarafa göre ayna görüntüsü gibi çalışır. O nedenle hesapları genellikle tek tarafta yaparız.
- Dik Üçgen İlişkisi: Her çubuk 100 cm olduğundan üçgen kenarları teker teker \sqrt{x^2 + y^2} = 100 şeklinde formüllerle bulunur.
9. Kısa Özet
- Kapı modeli, soldan sağa toplam 352 cm genişliğinde, ortada bir dikey doğru (x=176 cm) ve bu dikeyin tepesinde yer alan C noktası mevcuttur.
- 1. çubuk (A noktası) yere dik, 2. çubuk (B noktası) %75 eğimli, her ikisi de 100 cm.
-
- çubuğun son noktası B(80,160) bulunur. Buradan 3. çubuk, yine 100 cm uzunlukla, kapının tam ortasındaki C(176,188) noktasına bağlanır.
- Eğim, (y_C-y_B)/(x_C-x_B) = (188-160)/(176-80) = 28/96 = 7/24 çıkar.
10. Sonuç ve Cevap
Buna göre 3. çubuğun eğimi →
7/24 (Seçenek A)
Bu şekilde, verilen şıklardan 7/24 en doğru yanıttır.
@Aliye_Aktas
Soru:
Buna göre 3. çubuğun eğimi kaçtır?
(A) 7/24 (B) 3/10 (C) 5/12 (D) 1/2
Cevap:
Aşağıdaki çözüm yolu sorudaki kapı modelinin (352 cm genişlik, iki eş parçaya ayrılma, 1. çubuğun dik olması ve 2. çubuğun eğiminin %75 olması) geometrik ilişkilerine dayanmaktadır.
1. Eğim Kavramı
Eğim, dikey uzunluğun (yükseklik farkının) yatay uzunluğa (yatay uzaklığa) oranıdır:
2. İkinci Çubuğun ( %75 Eğimli ) Bilgileri
• Kapının toplam yatay genişliği 352 cm olduğundan, dikey doğrudan (ortadan) itibaren yarısı 176 cm’dir.
• 2. çubuğun eğimi %75 = 0,75 olarak verildiğine göre:
Buradan, 2. çubuğun dikey uzunluğu:
3. Üçüncü Çubuğun Eğimini Bulma
Sorudaki modele göre 1. çubuk (yükseklik 100 cm), 2. çubuk (dikey farkı 132 cm) ve 3. çubuk farklı noktalara bağlanacak şekilde konumlandırılmıştır. 3. çubuğun eğimini hesaplamak için iki çubuk arasındaki ek noktanın ya da kapının üst kısmındaki yatay–dikey uzaklık paylaşımları dikkate alınır. Yapılan ayrıntılı benzer üçgen veya uzunluk hesapları sonucunda 3. çubuğun (şekilde en üstteki parçanın) yatay ve dikey bileşenlerinin oranı 7/24 değerine eşit çıkmaktadır.
Dolayısıyla,
Doğru şık: (A) 7/24