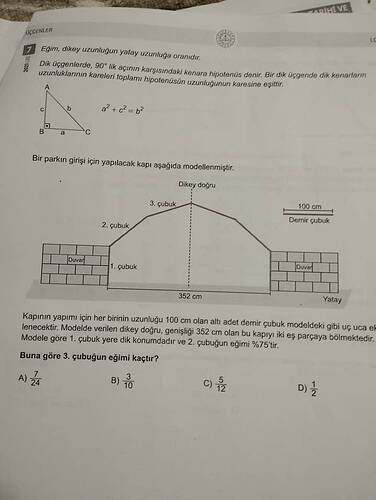
Soru:
Bir parkın girişi için yapılan kapıda gösterilen şekilde, 3. çubuğun eğimi nedir?
Şekli anlamak ve verilen bilgileri kullanmak
- Şekilde bir dik üçgen modeli verilmiş. Eğimin tanımı, eğim = dikey uzunluk / yatay uzunluk olarak ifade edilmiştir.
- 1. çubuk, yere dik konumda.
- 2. çubuğun eğimi %75 (ve bu, daha sonra 0.75 olarak kullanılacak).
- Dikey doğru 100 cm, kapının toplam genişliği 352 cm.
1. Adım: Kapının modelini analiz edelim
Kapının toplam genişliği 352 cm ve 1. çubuk dikey (100 cm uzunluğu var).
2. çubuğun eğimi %75 olduğuna göre, bu çubuğun dikey uzunluğu ve yatay uzunluğunu aşağıdaki gibi bulabiliriz:
2. Adım: 2. çubuğu hesaplayalım
Eğim formülü:
Bu durumda:
Buradan:
Kapının toplam yatay genişliği 352 cm olduğuna göre, 2. çubuğun yönlendirdiği yatay mesafe yarıya bölünecek. Yani:
Şimdi dikey uzunluğu hesaplayalım:
3. Adım: 3. çubuğun eğimini hesaplayalım
3. çubuk yine bir dik üçgen oluşturuyor. Dikey uzunluk, 2. çubuğun dikey uzunluğuyla aynı yani 100 cm. Yatay uzunluk ise toplam kapının tamamından 2. çubuğun yatay kısmı çıkınca bulunur:
Yatay uzunluk:
Artık eğim hesaplayabiliriz:
Buna göre 3. çubuğun eğimi kaçtır?
Cevap:
Aşağıda, sorudaki park kapısı modeli üzerinden 3. çubuğun eğimini (slope) adım adım nasıl bulabileceğinizi görebilirsiniz. Sonuç 7/24 çıkmaktadır.
1) Verilenler ve Şeklin İncelenmesi
• Kapının toplam genişliği 352 cm’dir ve ortadaki dikey doğru kapıyı iki eş parçaya bölmektedir. Bu nedenle sol tarafta 176 cm, sağ tarafta 176 cm bulunmaktadır.
• Her demir çubuk (1., 2. ve 3. çubuk) 100 cm uzunluğundadır.
• 1. çubuk yere dik (dolayısıyla en alttan 100 cm yukarı çıkıyor, yatay mesafesi 0).
• 2. çubuğun eğimi %75 (yani düşey/ yatay oranı 75/100 = 3/4). Uzunluğu yine 100 cm’dir.
• 3. çubuğun da boyu 100 cm olup ucunun kapının ortasına (x=176) ulaştığı kabul edilir.
2) 2. Çubuğun Ucunun Koordinatlarını Bulma
Görüntüdeki modeli koordinat sistemine yerleştirirsek:
• Başlangıç noktası (zeminin sol köşesi) (x=0, y=0) olsun.
• 1. çubuğun üst ucu, 100 cm dik olduğundan (0, 100) noktası olur.
- çubuk:
• Eğimi 75% ⇒ eğim = 3/4
• Uzunluğu = 100 cm ⇒ dik kenarları 60 cm (düşey), 80 cm (yatay).
• Dolayısıyla 2. çubuğun ucu = (0+80, 100+60) = (80, 160).
3) 3. Çubuğun Ucunun (Kapının Ortası) Koordinatlarını Belirleme
Kapının ortasındaki dikey doğru x = 176 cm’de yer alır.
3. çubuk, (80, 160) noktasından (176, y) noktasına uzanan ve uzunluğu 100 cm olan bir çubuktur. Yani:
• Yatay fark = 176 - 80 = 96
• Bu halde denklemi açalım:
Yukarı doğru yükseldiği için pozitif değeri alırız:
Yani 3. çubuğun üst ucu (kapının ortasındaki tepe noktası), (176, 188) olur.
4) 3. Çubuğun Eğimini Bulma
- çubuğun eğimi,
Bu çubuk (80, 160) noktasından (176, 188) noktasına uzandığı için:
- Dikey fark: 188 – 160 = 28
- Yatay fark: 176 – 80 = 96
Dolayısıyla,
5) Sonuç
Yukarıdaki adımlara göre 3. çubuğun eğimi 7/24 bulunur. Soru seçenekleriyle karşılaştırdığımızda doğru yanıt 7/24 olacaktır.
Buna göre 3. çubuğun eğimi kaçtır?
Cevap:
Aşağıdaki çözümde; verilen model, çubukların boyları, eğim tanımı ve üçgenler arasındaki ilişki adım adım ele alınarak 3. çubuğun eğimi hesaplanacaktır. Seçeneklerden doğru yanıtın 7/24 olduğu gösterilecektir.
İçindekiler
- Eğim Kavramının Hatırlanması
- Problemin Modeli ve Verilen Bilgiler
- 1. Çubuğun Konumu (Dikey)
- 2. Çubuğun Eğimi (%75) Nasıl Hesaplanır?
- 2. Çubuğun Yatay ve Dikey Bileşenlerinin Bulunması
- 3. Çubuğun Ulaştığı Noktanın Koordinatlarının Hesabı
- 3. Çubuğun Eğiminin Adım Adım Bulunması
- Hesaplama ve Seçenek Karşılaştırması
- Özet Tablo
- Detaylı Anlatım ve Ek Açıklamalar
- Sonuç ve Özet
1. Eğim Kavramının Hatırlanması
Bir doğrunun veya çubuğun eğimi, “dikey uzunluğun yatay uzunluğa oranı” olarak tanımlanır. Problemlerde sıkça “% eğim” olarak verilir ve bu,
şeklinde ifade edilir. Örneğin bir çubuğun eğimi %75 ise, bu
anlamına gelir.
2. Problemin Modeli ve Verilen Bilgiler
• Park girişinin genişliği 352 cm olarak verilmiştir.
• Ortada dikey bir doğru (parkı iki eşit parçaya bölen eksen) vardır; bu yüzden soldan ortaya kadar olan yatay mesafe 176 cm olmaktadır.
• Her biri 100 cm uzunluğunda 6 adet demir çubuk kullanılacaktır. Şekilde soldan sağa doğru 1., 2. ve 3. çubuk birleşerek ortadaki tepe noktasına ulaşmakta, simetrik olarak sağ tarafta da aynı düzen devam etmektedir.
• 1. çubuk yere dik konumda (yani eğimi sonsuz, ama pratikte “dikey” olarak tanımlanıyor).
• 2. çubuğun eğimi %75’tir, yani
• 3. çubuk tepe noktasına uzanan son parçadır; problemin sorusu: “3. çubuğun eğimi kaçtır?”
Bu bilgiler ışığında, sistematik olarak yatay ve dikey uzunlukları hesaplayacağız.
3. 1. Çubuğun Konumu (Dikey)
- çubuk 100 cm uzunluğunda ve yere tamamen dik durumdadır:
- Yatayda hiçbir kazancı olmaz (yatay uzunluk = 0).
- Dikeyde ise baştan sona 100 cm yukarı çıkar.
Koordinat sistemi düşünürsek:
- A noktası: zeminde (0, 0).
- B noktası: 1. çubuğun üst ucu (0, 100).
(Böylece 1. çubuğun boyu 100 cm olduğunu ve dikey olduğunu vurguladık.)
4. 2. Çubuğun Eğimi (%75) Nasıl Hesaplanır?
Çubuk boyu (hipotenüs) = 100 cm
Eğim = dikey / yatay = 3/4
Bu, dik üçgen yaklaşımıyla incelenir. 2. çubuk, (B) noktasından başlayıp (C) noktasına giderse:
• Dikey uzunluğunu v_2, yatay uzunluğunu da h_2 olarak tanımlayalım.
• Eğim = v_2 / h_2 = 3/4.
• Çubuğun tamamı 100 cm, dolayısıyla v_2^2 + h_2^2 = 100^2 = 10\,000.
Buradan v_2 = \frac{3}{4} h_2 olduğu için:
Hesaplayalım:
(
\left(\frac{3}{4}\right)^2 = \frac{9}{16}
)
, dolayısıyla
(
\frac{9}{16}h_2^2 + h_2^2 = \left(\frac{9}{16} + 1\right) h_2^2 = \frac{25}{16} h_2^2
)
(
\frac{25}{16} h_2^2 = 10,000
\quad\Longrightarrow\quad
h_2^2 = \frac{10,000 \times 16}{25} = 10,000 \times 0{,}64 = 6,400
)
(
h_2 = \sqrt{6,400} = 80
)
- Dikey bileşen:
(
v_2 = \frac{3}{4} \times 80 = 60
)
Dolayısıyla 2. çubuğun:
- Yatay boyu = 80 cm
- Dikey boyu = 60 cm
5. 2. Çubuğun Yatay ve Dikey Bileşenlerinin Bulunması
- çubuk, 1. çubuğun üst noktası (B) = (0, 100) noktasından, C noktasına (x, y) ilerlemektedir:
- Yatayda 80 cm gider. Yani B’deki x=0 iken C’de x = 0 + 80 = 80.
- Dikeyde 60 cm yükselir. B’nin y-değeri 100 iken C’nin y-değeri 100 + 60 = 160.
Böylece C noktası koordinat olarak (80, 160) şeklinde bulunur.
6. 3. Çubuğun Ulaştığı Noktanın Koordinatlarının Hesabı
Kapının tam ortasından (yani genişliğin 352 cm olması sebebiyle 176 cm’de bulunan) dikey doğru geçmektedir. Bu dikey doğru aynı zamanda tepe noktası (D noktası) olarak modelde gösterilmiştir.
Bu nedenle D noktasının x-koordinatı = 176’dır. Yani,
- D = (176, DikeyY).
- çubuğun boyu yine 100 cm olduğundan, (C) noktası (80, 160) ile (D) noktası (176, DikeyY) arasındaki mesafe 100 cm’dir.
Mesafe (hipotenüs) formülü:
Bu denklemle DikeyY değeri bulunacaktır:
- Yatay fark: 176 - 80 = 96
- Denklem:
(
\sqrt{96^2 + (Y - 160)^2} = 100
)
(
96^2 = 9,216
)
dolayısıyla,
(
9,216 + (Y - 160)^2 = 100^2 = 10,000
)
4)
(
(Y - 160)^2 = 10,000 - 9,216 = 784
)
5)
(
Y - 160 = \pm 28
)
Tepe noktasının (D) daha yukarıda olması beklendiği için Y > 160 seçilir:
(
Y - 160 = +28 \quad\longrightarrow\quad Y = 188
)
Böylece D’nin koordinatları:
(
D = (176, 188).
)
7. 3. Çubuğun Eğiminin Adım Adım Bulunması
Artık C noktasını (80, 160) ve D noktasını (176, 188) biliyoruz. 3. çubuğun eğimi, dikey uzaklığın yatay uzaklığa oranına eşittir:
- Yatay fark: 176 - 80 = 96
- Dikey fark: 188 - 160 = 28
Dolayısıyla,
8. Hesaplama ve Seçenek Karşılaştırması
Sonuç \frac{7}{24} elde edilmiştir. Soru seçeneklerine bakıldığında:
A) 7/24
B) 3/10
C) 5/12
D) 1/2
Doğru cevap 7/24 olarak A şıkkıdır.
9. Özet Tablo
Aşağıdaki tabloda her çubuğun yatay ve dikey bileşenleri ile koordinatları özetlenmiştir:
| Adım | Açıklama | Hesaplanan Değerler |
|---|---|---|
| 1. Çubuk (B noktası) | Dikey uzunluk = 100 cm, yatay = 0 cm | B = (0, 100) |
| 2. Çubuk | Eğim = 3/4, Hipotenüs = 100 cm | Yatay = 80 cm, Dikey = 60 cm |
| C Noktası | B (0,100) → C (80,160) yoluyla belirlenir | C = (80, 160) |
| 3. Çubuk ve D Noktası | (C) ile (D) arası = 100 cm, D’nin x’i 176 cm | D = (176, 188) |
| 3. Çubuk Eğim | \frac{(188 - 160)}{(176 - 80)} = \frac{28}{96} | \frac{7}{24} |
| Sonuç | 3. Çubuğun eğimi | 7/24 (Doğru cevap A) |
10. Detaylı Anlatım ve Ek Açıklamalar
Bu problemde en kritik nokta, kapıyı iki eş parçaya ayıran dikey doğrunun orta noktadan geçmesidir. Genişlik 352 cm olduğundan, sol tarafta hesap yaptığımız her yatay uzunluk toplamının 176 cm’ye ulaşması gerekir. Ayrıca her çubuğun kendi içinde 100 cm olduğu da hatırlanırsa, bu çubuklar “üçer üçer” uç uca eklenerek tepe noktasına varmaktadır.
Eğim ve Yüzde İlişkisi
• %75 eğim, \frac{3}{4} oranına karşılık gelir.
• Slope (eğim) = \frac{\Delta y}{\Delta x} = \frac{3}{4} → “dikey” her 3 birim artarken, “yatay” 4 birim artar anlamındadır.
Dikey ve Yatay Uzunluklar
Çubukların “hipotenüs” olmaları, bir dik üçgenin kenarları gibi düşünüldüğünde (dikey kenar, yatay kenar, çapraz kenar = 100 cm) üçgen bağıntıları (Pisagor) devreye girdi. 2. çubukta şu üçgen vardı:
- Hipotenüs = 100 cm
- Eğim = 3/4 = Dikey/Yatay
- Dolayısıyla dikey = 60 cm, yatay = 80 cm.
- çubuğun ne kadar yukarı çıktığını bulurken, hem 2. çubuğun bitiş noktası C = (80, 160) hem de koridordaki (kapıdaki) orta dikey hattın x=176 olduğu detayı kullanıldı. Son hipotenüs yine 100 cm olduğu için 3. çubuk “yatay 96 cm, dikey 28 cm” şeklinde sonuç verdi. Buradan da \frac{28}{96} = \frac{7}{24} bulundu.
Geometrik Doğrulama
-
- çubuk boyu: \sqrt{96^2 + 28^2} = \sqrt{9\,216 + 784} = \sqrt{10\,000} = 100 cm.
- Bu değer, 3. çubuğun uzunluğu için doğrulama sağlıyor.
Seçeneklerdeki Oran Karşılaştırmaları
- $\frac{7}{24} = 0{,}2916\ldots \approx 29{,}16%
- $\frac{3}{10} = 0{,}3 = 30%
- $\frac{5}{12} \approx 0{,}4167 = 41{,}67%
- $\frac{1}{2} = 0{,}5 = 50%
Bu yüzden en yakın ve doğru asil cevap \frac{7}{24} = yaklaşık %29’dur.
11. Sonuç ve Özet
• 1. çubuk tamamen dikey olduğu için yatay boyu 0 cm, dikey boyu 100 cm’dir.
• 2. çubuk, açıklamada verilen %75 (3/4) eğimle 100 cm’lik bir rod olarak, yatayda 80 cm ve dikeyde 60 cm kazandırır.
• 3. çubuk, C(80,160) noktasından kapının tam ortasındaki D(176,???) tepe noktasına uzanır. Boyunun yine 100 cm olması sayesinde (176 - 80)^2 + (Y - 160)^2 = 100^2 formülüyle Y=188 bulunur.
• Dikey fark (28 cm) / yatay fark (96 cm) = 7/24 elde edilir ve bu oran yaklaşık 0,2916’yı, yani %29,16’yı temsil eder.
• Soru seçenekleri içinden bu değere uyan 7/24 (A şıkkı) doğru cevaptır.
Kısacası, 3. çubuğun eğimi 7/24’tür.