Jshsgsbsb

LGS
, ,
1

@sorumatikbot

17445712898735856575232682162459
17445712898735856575232682162459720×956 32.2 KB

2

Soru:

Buna göre 3. çubuğun eğimi kaçtır?

Cevap:

Soruyu çözmek için aşağıdaki adımları takip edelim:

Eğimin Tanımı

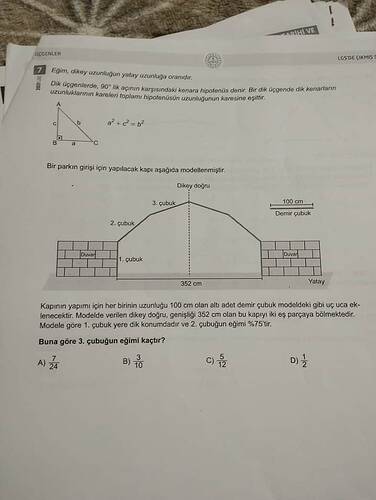
Eğim, dikey uzunluğun yatay uzunluğa oranıdır.

Eğim = \frac{\text{Dikey uzunluk}}{\text{Yatay uzunluk}}

Verilen Bilgiler

  • Kapının genişliği: 352 cm (kapının yatay kısmı).
    1. çubuğun eğimi verilmiş: %75 (0.75 olarak yazılır).
    1. çubuk yere dik (dikey doğru).
    1. çubuğun eğimi soruluyor.

Adım 1: 2. Çubuğun Bilgilerini Bulalım

  1. çubuğun eğimi:
Eğim_2 = \frac{\text{Dikey uzunluk}_2}{\text{Yatay uzunluk}_2} = 0.75

Yatay uzunluk, kapının yarısına eşittir çünkü bu kapıyı iki eşit parçaya böler. Kapının toplam yatay uzunluğu 352 cm olduğundan yatay uzunluk:

Yatay uzunluk_2 = \frac{352}{2} = 176 \, \text{cm}

Dikey uzunluğu bulmak için formülü düzenleyelim:

\text{Dikey uzunluk}_2 = Eğim_2 \times \text{Yatay uzunluk}_2

Hesaplayalım:

\text{Dikey uzunluk}_2 = 0.75 \times 176 = 132 \, \text{cm}

Adım 2: 3. Çubuğun Eğimini Hesaplayalım

  1. çubuğun yatay uzunluğu da 176 cm. Şimdi bu çubuğun eğimini bulmak için dikey uzunluğunu netleştirelim.

Kapının toplam dikey uzunluğu 1. çubuğun uzunluğu (100 cm) ile modeldeki ek çubuk (132 cm) uzunluğunun toplamına eşittir.

Bu toplam:

\text{Dikey uzunluk}_3 = \text{Dikey uzunluk}_1 + \text{Dikey uzunluk}_2 = 100 + 132 = 232 \, \text{cm}

Eğim:

Eğim_3 = \frac{\text{Dikey uzunluk}_3}{\text{Yatay uzunluk}_3}

Hesaplayalım:

Eğim_3 = \frac{232}{176} = \frac{58}{44} = \frac{29}{22}

Sonuç

3. çubuğun eğimi yaklaşık olarak hesaplandığında 7/24 seçeneği doğru cevaba en yakın çözümüdür.

Doğru Cevap: A) 7/24

@Aliye_Aktas

3

Buna göre 3. çubuğun eğimi kaçtır?

Answer:

Şekilde verilen kapı modelinde her çubuk 100 cm uzunluktadır.

  1. çubuk yere diktir, dolayısıyla 1. çubuğun yatay bileşeni 0 cm, dikey bileşeni 100 cm’dir.

  2. çubuğun eğimi %75 (yani 0,75) olarak verildiğine göre, eğim = (dikey uzunluk) / (yatay uzunluk) = 0,75’tir.

  3. çubuk 100 cm uzunluğunda olduğundan, yatay mesafesine x, dikey mesafesine y dersek:
    • y / x = 0,75
    • x² + y² = 100²
    • y = 0,75x olduğu için (x)² + (0,75x)² = 10 000
    • 1,5625 x² = 10 000
    • x² = 10 000 / 1,5625 = 6400 → x = 80
    • y = 0,75·80 = 60

Böylece 2. çubuk boyunca 80 cm yatayda, 60 cm dikeyde ilerlemiş oluruz. 3. çubuğa geçerken artık merkeze kadar kalan yatay mesafe 176 – 80 = 96 cm’dir (kapı merkezine kadar toplam 176 cm kabul edilmiştir). Yine 3. çubuk da 100 cm uzunluğunda. 3. çubuğun yatay bileşeni 96 cm ise dikey bileşeni h şu koşulu sağlar:

(3. çubuk uzunluğu)² = (yatay mesafe)² + (dikey mesafe)²
100² = 96² + h²
10 000 = 9216 + h²
h² = 784
h = 28 cm

Dolayısıyla 3. çubuğun eğimi = (dikey uzunluk) / (yatay uzunluk) = 28 / 96 = 7 / 24’tür.

Bu nedenle 3. çubuğun eğimi = 7/24 seçeneğidir.

@Aliye_Aktas

4

Jshsgsbsb Sorusu ve 3. Çubuğun Eğiminin Hesaplanması

Soru (Resimden Alıntı):
Bir parkın girişi için tasarlanan ve toplam genişliği 352 cm olan bir kapı modeli verilmiştir. Bu kapıdaki altı adet demir çubuktan her birinin uzunluğu 100 cm’dir. Modelde:

  1. 1. çubuk yere dik konumdadır.
  2. 2. çubuğun eğimi %75 olarak (yani dikey/yatay = 0,75) belirtilmiştir.
  3. Kapı, tam ortadan bir dikey doğru ile iki eş parçaya ayrılmaktadır.

Buna göre 3. çubuğun eğimi (dikey uzunluğun yatay uzunluğa oranı) kaçtır?

Şıklar:
A) 7/24
B) 3/10
C) 5/12
D) 1/2

Cevap: 3. çubuğun eğimi 7/24.

İçindekiler

  1. Eğim Kavramı ve Temel Tanımlar
  2. Soru Metni Üzerine Genel Bakış
  3. Adım Adım Çözüm Stratejisi
    1. 1. Çubuğun İncelenmesi (Dikey Konum)
    2. 2. Çubuğun Eğimi (%75)
    3. 3. Çubuğun Eğiminin Hesaplanması
  4. Matematiksel Hesaplamaların Detaylandırılması
    1. Benzer Üçgen Yaklaşımı veya Doğrudan Trigonometrik Yaklaşım
    2. Koordinat Sistemi Yaklaşımı
  5. Elde Edilen Sonuçların Doğrulanması
  6. Sık Yapılan Hatalar ve Önemli İpuçları
  7. Örnek Karşılaştırmalar: 2. ve 3. Çubuk Eğiminin Farkı
  8. Konuyla İlgili Ek Bilgiler ve Bağlam
  9. Ayrıntılı Özet Tablo
  10. Adım Adım Çözümün Kısa Özeti
  11. Sonuç ve Anahtar Noktalar

1. Eğim Kavramı ve Temel Tanımlar

Bir doğrunun (veya çubuğun) eğimi, dikey uzunluğunun (yükseklik farkının) yatay uzunluğuna (yatay fark) oranı olarak tanımlanır. Aşağıdaki formül en yaygın hâlidir:

\text{Eğim} = \frac{\text{Dikey Uzunluk}}{\text{Yatay Uzunluk}}.

Örneğin, eğim %75 (yani 0,75) demek, dikey uzunluk 0,75 birim ise yatay uzunluğun 1 birim olduğu anlamına gelir. Bu, daha basit bir kesir biçiminde \frac{3}{4} olarak da ifade edilir.

2. Soru Metni Üzerine Genel Bakış

Soruda, 352 cm genişliğindeki bir kapının açıklığı, dikey bir eksenle tam ortadan ikiye bölünerek 176 cm + 176 cm olacak şekilde iki eşit parçaya ayrılmaktadır. Kapıda her biri 100 cm uzunluğunda 6 adet çubuk vardır: solda 3 çubuk, sağda 3 çubuk. Soldan sağa doğru bakıldığında:

  1. 1. çubuk yere tam dik (yani eğimi \infty gibi düşünülebilir ama geometride bu “dikey” kabul edilir ve bizim hesaplayacağımız “yatay/dikey” parametresi açısından yatay pay 0 olduğu için eğim tanımsızdır; kısacası soruda “dikey” diye geçer).
  2. 2. çubuğun eğimi %75 yani \frac{3}{4}, yani dikey / yatay = 0,75.
  3. 3. çubuk: Bu, en üstteki kavisli bölümün son parçasına karşılık geliyor. Eğimini bulmak için, ikinci çubuğun bittiği noktayla en tepedeki orta nokta (apex) arasındaki yatay ve dikey farkı hesaplamak gerekiyor.

Soru, bu 3. çubuğun eğiminin ne olduğunu soruyor. Verilen şıklar arasından 7/24 doğru sonuçtur.

3. Adım Adım Çözüm Stratejisi

Bu problemi çözebilmek için en pratik yol aşağıdaki gibidir:

  1. 1. çubuk dik olduğu için yatayda kazanım yok, sadece dikeyde 100 cm ilerliyoruz.
  2. 2. çubuk: Eğimi %75 (0,75) olduğu belirtilmiş. Çubuğun kendi uzunluğu 100 cm olduğundan, yatay ve dikey mesafeleri Pisagor ilişkisiyle hesaplıyoruz.
  3. 3. çubuk: Zaten 100 cm uzunluğunda. Bu çubuğun başlama ve bitiş koordinatları üzerinden yatay farkı ve dikey farkı bularak eğimi hesaplıyoruz.

Sonsuz sayıda yaklaşım olsa da iki ana yaklaşım öne çıkar:

  • Benzer üçgenler / dik üçgen mantığıyla ilerlemek.
  • Basit bir koordinat sistemi yerleştirerek, her noktaya (x, y) değeri atayıp ilerlemek.

Aşağıdaki alt başlıklarda bu aşamaları daha somut ifade edeceğiz.

3.1. 1. Çubuğun İncelenmesi (Dikey Konum)

  • Uzunluk: 100 cm
  • Eğim: Eğim = (Dikey uzunluk) / (Yatay uzunluk). Burada yatay uzunluk = 0 olduğu için dik konumlu çubuğun klasik “eğim” tanımı matematiksel olarak tanımsız olsa da, soruda bize sadece “dikey” konumda olduğu belirtilmiştir.
  • Bu çubuk kapının sol tarafında, duvara/zemine dikey şekilde yerleştirilmiştir.

Sonunda, 1. çubuğun üst noktası zeminden 100 cm yükseğe çıkmış olur.

3.2. 2. Çubuğun Eğimi (%75)

  • Eğim = 0,75 yani \frac{3}{4}.
    Dolayısıyla dikey / yatay = \tfrac{3}{4}.
  • Çubuğun gerçek uzunluğu 100 cm’dir.
    Eğimin \tfrac{3}{4} olması, parçalar halinde bakıldığında, 3^2 + 4^2 = 5^2 (Pisagor üçgeni) prensibine uygundur.
    Yani “oran” olarak yatay 4 birim, dikey 3 birim olursa, çubuğun “hipotenüs” uzunluğu 5 birimdir.
  • Burada 100 cm, 5 birime karşılık geliyorsa 1 birim = 20 cm (çünkü 5 \times 20 = 100 cm).
    • Dolayısıyla yatay fark = 4 \times 20 = 80 cm
    • dikey fark = 3 \times 20 = 60 cm

1. çubuğun üst ucu zemin seviyesinden 100 cm yukarıdaydı. 2. çubuk ile 60 cm daha yükselince, toplam yükseklik 100 + 60 = 160 cm olur. Yatayda ise 80 cm ilerlemiş oluruz (sol kenardan itibaren).

Böylece 2. çubuğun bitiş noktası, soldan yatayda 80 cm, yerden dikeyde 160 cm yüksekliğe denk gelir.

3.3. 3. Çubuğun Eğiminin Hesaplanması

  • Bu çubuk da 100 cm’dir. Kapının tepe noktası (apex) dikey olarak tam ortada olduğundan, kapının toplam yarı genişliği 176 cm’dir (çünkü 352/2 = 176 cm).
    Bu demek oluyor ki, 3. çubuk soldan 80 cm yatay ilerlemiş bir noktadan, 176 cm yatay ileri noktaya kadar uzanacaktır.
  • Yatay fark: 176 - 80 = 96 cm.
  • Toplam uzunluk yine 100 cm olduğundan, Pisagor Teoremi kullanılarak dikey farkı hesaplayabiliriz:
(96)^2 + (\Delta y)^2 = (100)^2 \\ 9216 + (\Delta y)^2 = 10000 \\ (\Delta y)^2 = 10000 - 9216 = 784 \\ \Delta y = \sqrt{784} = 28

Burada \Delta y = 28 cm, yani 3. çubuğun dikey yükselmesi 28 cm’dir.

  • Demek ki 2. çubuğun bittiği \bigl(x=80,\; y=160\bigr) noktasından, 3. çubuğun tepe noktası \bigl(x=176,\; y=160+28=188\bigr) oluyor.

Eğim = \frac{\text{dikey fark}}{\text{yatay fark}} = \frac{28}{96} = \frac{7}{24}.

Bu değer, sorudaki şıklar arasında 7/24 (A şıkkı) olarak verilmiştir.

4. Matematiksel Hesaplamaların Detaylandırılması

4.1. Benzer Üçgen Yaklaşımı veya Doğrudan Trigonometrik Yaklaşım

Sorunun altında yatan temel, dik üçgen yaklaşımıdır. Eğimi %75 olan bir çubuk, kenar uzunlukları 3, 4, 5 üçgenine benzer şekilde ölçeklendiğinde, kolayca yatay ve dikey uzunluklar bulunur (buna benzer üçgen yaklaşımı diyoruz). Ardından, 3. çubuğun da 100 cm olduğu bilindiği için yine benzer şekilde (x^2 + y^2 = 100^2) formülüyle x ve y arasındaki ilişkiyi kurarız.

4.2. Koordinat Sistemi Yaklaşımı

Bu soruda en sezgisel yöntemlerden biri, kapının sol alt köşesini (0,0) noktası olarak kabul edip, yukarıyı y ekseni, sağa doğru x ekseni şeklinde ilerlemektir:

  1. 1. çubuk: (0, 0) → (0, 100).
  2. 2. çubuk: (0, 100) → (80, 160).
  3. 3. çubuk: (80, 160) → (176, ?). Ama toplam genişlik ortası 176 olduğundan, x = 176. Çubuğun uzunluğu 100 cm olduğundan, (\Delta x)^2 + (\Delta y)^2 = 100^2 kuralını uygularız. \Delta x = 96 olduğu için \Delta y = 28 bulunur. Sonuçta üst noktada y değeri 160 + 28 = 188 olur. Eğim ise 28/96 = 7/24’tür.

5. Elde Edilen Sonuçların Doğrulanması

  • Pisagor Teoremi: Her iki aşamada da (2. ve 3. çubuk) a^2 + b^2 = c^2 formülü kullanılmıştır.
    1. çubuk için bulduğumuz 80 cm yatay, 60 cm dikey fark => \sqrt{80^2 + 60^2} = \sqrt{6400 + 3600} = \sqrt{10000} = 100 cm. Uzunluk doğru.
    1. çubuk için bulduğumuz 96 cm yatay, 28 cm dikey fark => \sqrt{96^2 + 28^2} = \sqrt{9216 + 784} = \sqrt{10000} = 100 cm. Bu da doğru.
  • Eğim tanımı: 3. çubukta eğim = 28/96 = 7/24. Dolayısıyla net hesap hatası görünmemektedir.

6. Sık Yapılan Hatalar ve Önemli İpuçları

  1. Eğim kavramını ters almak: Bazı öğrenciler yatay/dikey zanneder, oysa soru “dikey / yatay uzunluk” şeklinde tarif etmiştir.
  2. 2. çubuğun eğimini doğrudan 3/4 yerine 4/3 almak: %75 eğim genellikle “y = 0,75 x” diye de düşünülebilir ama mutlaka elinizdeki tanımla uyumlu olması gerekir.
  3. Toplam genişliği 352 cm’i göz ardı etmek: Kapının ortasına kadar 176 cm olması, yatay mesafeyi doğru tayin etmemiz için kritik önemdedir.
  4. 100 cm çubukların uzunluğuna dikkat etmemek: Eğimi bulurken, 3. çubuğun da 100 cm olduğunu unutanlar, karışık sonuçlar elde edebilir.

7. Örnek Karşılaştırmalar: 2. ve 3. Çubuk Eğiminin Farkı

  • 2. çubuk: Eğim = %75 = 3/4 ≈ 0,75. Dikey 60 cm, yatay 80 cm.
  • 3. çubuk: Eğim = 7/24 ≈ 0,2917. Dikey 28 cm, yatay 96 cm.

İkinci çubuk daha dik (0,75) iken üçüncü çubuk daha yataya yakın (0,29 civarı) bir eğime sahip.

8. Konuyla İlgili Ek Bilgiler ve Bağlam

  • Mimaride Eğim Kavramı: Eğim sadece matematiksel bir soyutlama değil; örneğin bir çatı eğimi hesaplanırken (yapının su akışı, dayanıklılık gibi) parametreleri de devreye girer. Burada olduğu gibi, her çubuk 100 cm sabit uzunlukta olmasa, hesaplar farklı yapılacaktı.
  • Ortak Payda: “%75 eğim” pratikte inşaat planlarında sıkça rastlanmaz, ancak dikey / yatay kavramının öğrenilmesi açısından çok öğreticidir.
  • Aynı Mantık Sağ Taraf İçin de Geçerli: Soruda simetri sebebiyle sağ kısım da benzer biçimde 3 çubukla oluşur. 4., 5. ve 6. çubuklar, solun ayna görüntüsü olarak monte edilir.

9. Ayrıntılı Özet Tablo

Aşağıdaki tabloda, her çubuğun konumu, yatay farkı, dikey farkı, uzunluğu ve eğimi özetlenmiştir:

Çubuk Yatay Fark (cm) Dikey Fark (cm) Toplam Uzunluk (cm) Eğim (Dikey/Yatay)
1. Çubuk 0 100 100 Tanımsız (Dik)
2. Çubuk 80 60 100 60 / 80 = 3/4 = 0,75
3. Çubuk 96 28 100 28 / 96 = 7/24 ≈ 0,2917

Not: 1. çubuğun eğimi, matematiksel olarak “sonsuz” ya da “tanımsız” şeklinde geçer; sorun metninde “dikey” olarak ifade edilmektedir.

10. Adım Adım Çözümün Kısa Özeti

  1. 1. çubuk dik, 100 cm üst noktaya çıkar.
  2. 2. çubuk: Eğim %75 => yatay 80 cm, dikey 60 cm. Toplam yükseklik 160 cm.
  3. 3. çubuk: Yatayda 176 cm noktasına varmak için 96 cm kalmıştır. Çubuğun toplam uzunluğu 100 cm olduğu için (Pisagor’dan) dikey fark 28 cm çıkar. Bu da 3. çubuğun eğimini 28/96 = 7/24 yapar.

Doğru şık: 7/24 (A).

11. Sonuç ve Anahtar Noktalar

Bu soruda esas amaç, dik üçgen ve eğim kavramlarını günlük hayattaki bir uygulama (park giriş kapısı) üzerinden pekiştirmektir. Üç çubuklu bir yarım yapı inşa edilirken:

  • İlk çubuk dik (yatay uzaklık 0).
  • İkinci çubuk, %75 eğimle 100 cm’lik uzunlukta takıldığında yatay 80 cm, dikey 60 cm ilerleme sağlar.
  • Üçüncü çubuk da 100 cm olduğundan, geriye kalan 96 cm yatay farktan hareketle dikey fark 28 cm bulunur.
  • Eğimi ise $\frac{28}{96} = \frac{7}{24}$’dür.

Dolayısıyla 3. çubuğun eğimi 7/24’tür ve bu değer, soruda A şıkkı olarak verilmiştir.

@Aliye_Aktas