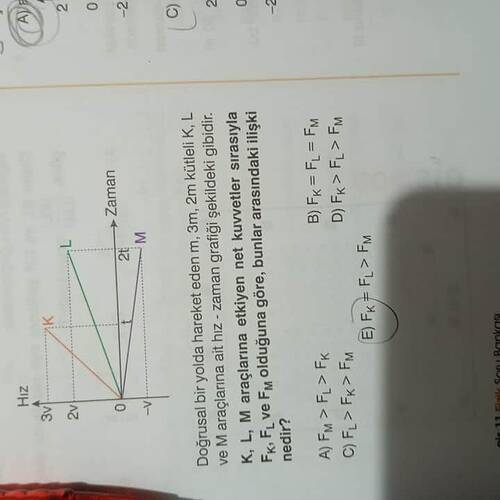
Doğrusal bir yolda hareket eden m, 3m, 2m kütleli K, L ve M araçlarına ait hız-zaman grafiği verilmiştir. Bu araçlara etkiyen net kuvvetler sırasıyla F_K, F_L, ve F_M olduğuna göre, bunlar arasındaki ilişki nedir?
Cevap:
Öncelikle hız-zaman (v-t) grafiği üzerinden hareketlerin ivmelerini bulmamız gerekmektedir. İvme (a), hız değişiminin zaman değişimine bölünmesiyle bulunur. Yani, ivme formülü şu şekildedir:
a = \frac{\Delta v}{\Delta t}
Her bir araç için ivmeyi bularak kuvvetleri karşılaştırabiliriz, çünkü Newton’un 2. Yasası’na göre net kuvvet (F), kütle (m) ile ivmenin çarpımına eşittir:
F = m \cdot a
Adım Adım Çözüm:
-
K Aracı:
- Başlangıç hızı 3v, final hızı 0, zaman t.
- \Delta v_K = 0 - 3v = -3v, \Delta t = t.
- a_K = \frac{-3v}{t}.
- Kütlesi: m_K = m.
- Kuvvet: F_K = m \cdot \left(\frac{-3v}{t}\right) = \frac{-3mv}{t}.
-
L Aracı:
- Başlangıç hızı 2v, final hızı 0, zaman 2t.
- \Delta v_L = 0 - 2v = -2v, \Delta t = 2t.
- a_L = \frac{-2v}{2t} = \frac{-v}{t}.
- Kütlesi: m_L = 3m.
- Kuvvet: F_L = 3m \cdot \left(\frac{-v}{t}\right) = \frac{-3mv}{t}.
-
M Aracı:
- Başlangıç hızı 0, final hızı -v, zaman 2t.
- \Delta v_M = -v - 0 = -v, \Delta t = 2t.
- a_M = \frac{-v}{2t}.
- Kütlesi: m_M = 2m.
- Kuvvet: F_M = 2m \cdot \left(\frac{-v}{2t}\right) = \frac{-mv}{t}.
Kuvvetlerin Karşılaştırılması:
- F_K = \frac{-3mv}{t}
- F_L = \frac{-3mv}{t}
- F_M = \frac{-mv}{t}
Bu değerlerden şunu görürüz:
F_K = F_L > F_M, bu durumda seçeneklerden hangisinin bu ilişkileri doğru belirttiğini kontrol edersek:
Sonuç:
Doğru cevap B) F_K = F_L > F_M seçeneğidir.