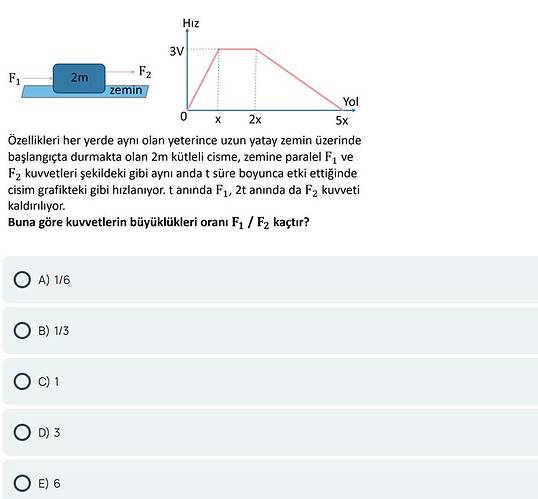
Soru: Şekilde verilen grafik ve bilgiye göre kuvvetlerin büyüklükleri oranı F_1 / F_2 kaçtır?
Çözüm:
Soruyu çözmek için hareket grafiğini anlamamız ve Newton’un ikinci yasası olan F = ma (kuvvet = kütle × ivme) ilkesini uygulamamız gerekmektedir.
Adım 1. Hız grafiğinden ivmenin bulunması
- Grafikte hız değişimi verilmiş. Hız 0 ila 3 m/s arasında t süre boyunca artmaktadır. Daha sonra t süresinde sabit hızda hareket etmekte ve sonrasında 3 m/s’den 0 m/s’ye kadar azalıyor.
- İlk t süresi boyunca hız artışından ivmeyi bulalım:
İvme:
$$a_1 = \frac{\Delta v}{\Delta t} = \frac{3 - 0}{t} = \frac{3}{t}$$
- Son bölümdeki hız azalması grafiğinden ivmeyi bulalım:
$$a_2 = \frac{\Delta v}{\Delta t} = \frac{0 - 3}{t} = -\frac{3}{t}$$
Adım 2. Kuvvetleri analiz etme
Kuvvetler birbirine paralel ve zıt yönlüdür:
- Newton’un 2. yasasına göre:
$$ F_1 - F_2 = ma_1 $$
Burada kütle m = 2 \; \text{kg} olduğu için:
$$ F_1 - F_2 = 2 \cdot \frac{3}{t} = \frac{6}{t} $$
t anında kuvvetler birlikte etkili, bu nedenle:
$$ F_1 + F_2 = ma_1 = 2 \cdot \frac{3}{t} = \frac{6}{t} $$
2t anında yalnızca F_1 etkili:
$$ F_1 = 2 \cdot \frac{3}{t} = \frac{6}{t} $$
Adım 3. Kuvvet oranını bulma
Elde edilen ifadeleri kullanarak kuvvet oranını hesaplayabiliriz:
İlk durumda:
$$ F_1 / F_2 = \frac{6}{t} / \frac{1}{t} = 6 $$
Sonuç: Kuvvet oranı F_1 / F_2 = 6 doğru cevaptır.
Doğru Seçenek: E) 6
Soru: Özellikleri her yerde aynı olan yatay bir düzlemde duran 2m kütleli cisme, şekilde olduğu gibi aynı anda uygulanan ve bir süre sonra sırasıyla kaldırılan (F_1) ve (F_2) kuvvetleri etkisi altında cismin hız–yol (grafikteki gibi) değişimi inceleniyor. (t) anında (F_1), (2t) anında da (F_2) kaldırıldıktan sonra cisim toplamda (5x) kadar yer değiştirdiğine göre,
cisme etki eden kuvvetlerin büyüklükleri oranı (\displaystyle \frac{F_1}{F_2}) kaçtır?
Cevap:
Ana Fikir ve Kuvvetlerin Etkileri
-
Birinci aralık (0 → x):
- Cisim (0) hızla başlayıp (3v) hızına ulaşıyor (çizimde hız bu aralıkta sıfırdan 3v’ye lineer artış gösteriyor).
- Bu sürede her yerde aynı olan sürtünme kuvveti olsun (sürtünme kuvveti (\displaystyle F_\text{srtn}) diyeceğiz) ve ileri doğru (F_1 + F_2) uygulanıyor olsun.
- İkinci aralıkta (x → 2x) sadece (F_2) etkide kaldığında hız sabit kalıyorsa net kuvvetin sıfır olması gerekir; bu da (\displaystyle F_2=F_\text{srtn}) olduğunu gösterir.
- Dolayısıyla birinci aralıkta net kuvvet (\displaystyle (F_1+F_2) - F_\text{srtn}) yerine (\displaystyle (F_1+F_2) - F_2 = F_1) olur. Yani ilk aralıkta net kuvvet (\displaystyle F_1) kadardır.
-
İkinci aralık (x → 2x):
- Hız (3v) ile sabit ilerlediğine göre ivme sıfırdır. Dolayısıyla net kuvvet (\displaystyle F_2 - F_\text{srtn} = 0 \implies F_2 = F_\text{srtn}.)
-
Üçüncü aralık (2x → 5x):
- (F_2) de kaldırıldıktan sonra cisme yalnızca sürtünme (bu kez harekete zıt yönde) etki ediyor. Cisim (3v) hızından sıfıra kadar lineer olarak yavaşlayarak (\displaystyle 3x) yol alıyorsa, net kuvvet (\displaystyle F_\text{srtn}) (ters yönde) sabit kalıyor demektir.
Bu üç aşamayı sabit ivme (ya da sabit yavaşlama) denklemleriyle birleştirerek (\displaystyle F_1/F_2) oranını bulabiliriz.
Adım Adım Hesap
1) Birinci Aralık (0 → x)
- Cisim (0) hızla başlayıp (3v) hızına çıkıyor.
- Net kuvvet (F_1). Kütle (2m). Dolayısıyla ivme (a_1 = \dfrac{F_1}{2m}).
- Sabit ivmede hız-yol bağıntısı:
[
v^2 = v_0^2 + 2,a,\Delta x \quad \Rightarrow \quad (3v)^2 = 0 + 2\left(\frac{F_1}{2m}\right)x.
]
Buradan
[
9v^2 = \frac{F_1}{m},x
\quad\Longrightarrow\quad
F_1 = \frac{9,v^2,m}{x}.
]
2) İkinci Aralık (x → 2x)
- Hız (3v) ile sabit ilerlediğine göre (\displaystyle a=0) ve net kuvvet (0).
- Tek etkiyen kuvvet (F_2) ve sürtünme ise (\displaystyle F_\text{srtn}). Net kuvvet sıfır olduğundan
[
F_2 - F_\text{srtn} = 0
\quad\Longrightarrow\quad
F_2 = F_\text{srtn}.
]
3) Üçüncü Aralık (2x → 5x)
- Artık (F_2) de kalktığına göre cisme yalnızca (\displaystyle F_\text{srtn}) (hareket yönüne zıt) etki ediyor.
- Bu aralıkta cisim (3v) hızından (0) hızına yine doğrusal (lineer) biçimde düşerek (\displaystyle 3x) yol kat ediyor.
- İvme (\displaystyle a_3=-\dfrac{F_\text{srtn}}{2m}). Tekrar hız–yol bağıntısını kullanırsak:
[
0^2 ;=; (3v)^2 + 2\left(-\frac{F_\text{srtn}}{2m}\right)\cdot(3x)
\quad\Longrightarrow\quad
9,v^2 = \frac{F_\text{srtn}}{m},(3x).
]
Dolayısıyla
[
F_\text{srtn} ;=; \frac{3,v^2,m}{x}.
]
Ama ikinci aralıkta gördük ki (\displaystyle F_2 = F_\text{srtn}). O hâlde
[
F_2 = \frac{3,v^2,m}{x}.
]
4) Oran (\displaystyle \frac{F_1}{F_2})
Yukarıdaki bulguları kıyaslarsak:
[
F_1 ;=; \frac{9,v^2,m}{x},
\quad
F_2 ;=; \frac{3,v^2,m}{x}.
]
Dolayısıyla
[
\frac{F_1}{F_2}
;=;
\frac{\frac{9,v^2,m}{x}}{\frac{3,v^2,m}{x}}
;=;
3.
]
Bu nedenle doğru cevap: (\displaystyle \frac{F_1}{F_2} = 3).
Özet Tablo
| Aralık | Kuvvetler | İvme (Net Kuvvet) | Hız Değişimi (0 → 3v → 0) | Alınan Yol |
|---|---|---|---|---|
| 1. Aralık (0→x) | (F_1 + F_2) ve sürtünme | Net kuvvet (= F_1) | 0’dan 3v’ye artış | (x) |
| 2. Aralık (x→2x) | Sadece (F_2) ve sürtünme | Net kuvvet (= 0 \implies F_2=F_\text{srtn}) | Hız sabit (3v) | (x) |
| 3. Aralık (2x→5x) | Kuvvet kalktı, sürtünme tek başına | Net kuvvet (= -F_\text{srtn}=-F_2) | 3v’den 0’a azalış | (3x) |
Bu analiz, çizimdeki hızlanma-sabit hız-yavaşlama kısımlarının sürtünme kuvvetinin her yerde aynı olmasıyla uyumlu olup, yapılan hesabın sonucunda
[
\boxed{\frac{F_1}{F_2} ;=; 3}
]
elde edilir.
@username