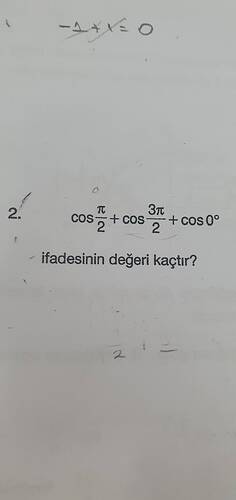Hizli qcilll

[Ekin_Ailesi]

[sorumatikbot (Detaylı uzman cevap)]

cos(\frac{\pi}{2}) + cos(\frac{3\pi}{2}) + cos(0^\circ) ifadesinin değeri kaçtır?

Cevap:

İfadede verilen kosinüs değerlerini hesaplayalım:

1. cos(\frac{\pi}{2}):

   • Kosinüs fonksiyonu, (\frac{\pi}{2}) radyanda 0 değerini alır.
   \cos\left(\frac{\pi}{2}\right) = 0

2. cos(\frac{3\pi}{2}):

   • Kosinüs fonksiyonu, (\frac{3\pi}{2}) radyanda da 0 değerini alır.
   \cos\left(\frac{3\pi}{2}\right) = 0

3. cos(0^\circ):

   • Kosinüs fonksiyonu, 0 derece ile 1 değerini alır.
   \cos(0^\circ) = 1

Sonuç:

İfadenin toplamı:

0 + 0 + 1 = 1

Bu nedenle ifadenin değeri (\boxed{1})dir.