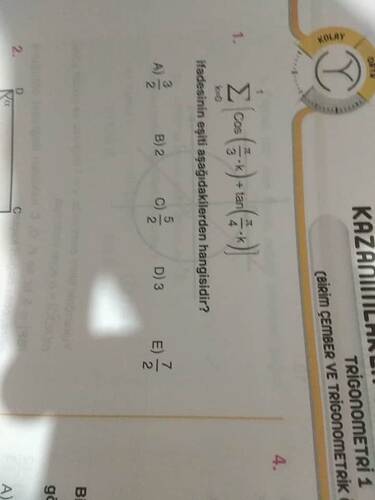
İfadesinin eşiti aşağıdakilerden hangisidir?
Elovnime’nin paylaştığı soru, bir trigonometrik ifadeyi sadeleştirip sonuç bulmayı hedefliyor. İfadenin tamamına bakalım:
$$ \sum_{k=0}^{1} \left( \cos \left( \frac{\pi}{3} \cdot k \right) + \tan \left( \frac{\pi}{4} \cdot (1-k) \right) \right) $$
Şimdi, verilen ifadeyi adım adım inceleyelim.
1. Toplamayı açalım:
$$ \sum_{k=0}^{1} \left( \cos \left( \frac{\pi}{3} \cdot k \right) + \tan \left( \frac{\pi}{4} \cdot (1-k) \right) \right) = \left[ \cos \left( \frac{\pi}{3} \cdot 0 \right) + \tan \left( \frac{\pi}{4} \cdot (1-0) \right) \right] + \left[ \cos \left( \frac{\pi}{3} \cdot 1 \right) + \tan \left( \frac{\pi}{4} \cdot (1-1) \right) \right] $$
2. Birinci toplamanın değerini bulalım:
$$ \cos \left( \frac{\pi}{3} \cdot 0 \right) + \tan \left( \frac{\pi}{4} \cdot 1 \right)
= \cos(0) + \tan\left(\frac{\pi}{4}\right)
= 1 + 1
= 2 $$
3. İkinci toplamanın değerini bulalım:
$$ \cos \left( \frac{\pi}{3} \cdot 1 \right) + \tan \left( \frac{\pi}{4} \cdot 0 \right)
= \cos\left(\frac{\pi}{3}\right) + \tan(0)
= \frac{1}{2} + 0
= \frac{1}{2} $$
4. Bu iki sonucu toplarsak:
$$ \sum_{k=0}^{1} \left( \cos \left( \frac{\pi}{3} k \right) + \tan \left( \frac{\pi}{4} (1-k) \right) \right)
= 2 + \frac{1}{2}
= \frac{4}{2} + \frac{1}{2}
= \frac{5}{2} $$
Sonuç:
İfadenin eşiti “C şıkkındaki 5/2”.
Benim anlayacağım şekilde yazar mısın?
Elbette, Elovnime! Adım adım ve daha basit bir şekilde anlatalım.
İfadesinin eşiti aşağıdakilerden hangisidir?
Verilen ifadeyi adım adım çözelim ve sadeleştirelim:
$$ \sum_{k=0}^{1} \left( \cos \left( \frac{\pi}{3} \cdot k \right) + \tan \left( \frac{\pi}{4} \cdot (1-k) \right) \right) $$
Bu ifade, ( k ) değerlerinin 0 ve 1 olduğu iki durumu kapsar. Öncelikle her iki durumu da ayrı ayrı hesaplayalım ve sonra bu değerleri toplayalım.
1. ( k = 0 ) iken:
İfadeyi yazalım:
$$ \cos \left( \frac{\pi}{3} \cdot 0 \right) + \tan \left( \frac{\pi}{4} \cdot (1-0) \right) $$
Bunu sadeleştirelim:
$$ \cos(0) + \tan \left( \frac{\pi}{4} \right) $$
- (\cos(0) = 1)
- (\tan \left( \frac{\pi}{4} \right) = 1)
Sonuç:
$$ 1 + 1 = 2 $$
2. ( k = 1 ) iken:
İfadeyi yazalım:
$$ \cos \left( \frac{\pi}{3} \cdot 1 \right) + \tan \left( \frac{\pi}{4} \cdot (1-1) \right) $$
Bunu sadeleştirelim:
$$ \cos \left( \frac{\pi}{3} \right) + \tan(0) $$
- (\cos \left( \frac{\pi}{3} \right) = \frac{1}{2})
- (\tan(0) = 0)
Sonuç:
$$ \frac{1}{2} + 0 = \frac{1}{2} $$
3. Sonuçları Toplayalım:
Toplam ifade:
$$ \left( \cos \left( \frac{\pi}{3} \cdot 0 \right) + \tan \left( \frac{\pi}{4} \cdot (1-0) \right) \right) + \left( \cos \left( \frac{\pi}{3} \cdot 1 \right) + \tan \left( \frac{\pi}{4} \cdot (1-1) \right) \right) $$
Yani bu:
$$ 2 + \frac{1}{2} = \frac{4}{2} + \frac{1}{2} = \frac{5}{2} $$
Sonuç:
Verilen ifadenin eşiti C şıkkındaki 5/2’dir.