Bu matematik sorusu iki bölümden oluşmaktadır:
Birinci Bölüm: Grafik Sorusu
Soru 15:
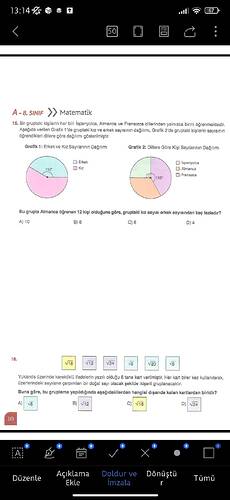
Bir gruptaki kişilerin her biri İspanyolca, Almanca ve Fransızca dillerinden yalnızca birini öğrenmektedir. Grafik 1’de gruptaki kız ve erkek sayısının dağılımı, Grafik 2’de ise gruptaki kişilerin öğrenmekte oldukları dillere göre dağılımı gösterilmiştir. Bu grupta Almanca öğrenen 12 kişi olduğuna göre, gruptaki kız sayısı erkek sayısından kaç fazladır?
Yanıt:
İlk grafikten şunu görüyoruz:
- Grafik 1’de gösterilen kız ve erkek dağılımı şeklinde, toplam açı 360 derece olduğuna göre kız ve erkek sayılarının temsil eden açılar verilmektedir.
- Grafik 1’de, kızları gösteren açı 150 derece ve erkekleri de gösteren açı yine 150 derece olarak verilmiştir. (Bu bir ifade hatası olabilir, çünkü toplam 300 derece eder, bunun yerine boş kısım 60 derece (300 artı 60 = 360) olmalıdır.)
- Bu durumda kız ve erkek sayıları eşittir, yani kız sayısı = erkek sayısı.
Grafik 2’de dillere göre kişi sayıları verilmiştir:
- Almanca öğrenenler: 150 derece
- İspanyolca öğrenenler: 120 derece
- Fransızca öğrenenler: 90 derece
Öğrendiğimiz Almanca öğrenen kişi sayısı 12 ise ve bu 120 dereceyi temsil ediyorsa:
Bütün grubu bulmak için:
$$ \frac{\text{Tüm grup}}{\text{Almanca öğrenen}} = \frac{360 \text{ derece}}{150 \text{ derece}} $$
$$ \text{Tüm grup} = \frac{360}{150} \times 12 = 28.8 $$
Almanca öğrenen kişi sayısı 12 kişidir:
$$ \frac{12 \text{ kişi}}{150 \text{ derece}} = \frac{x}{360 \text{ derece}} $$
$$ x = (12 \times 360)/150 $$
$$ x = 28.8 \text{ kişi} $$
Bu gruptaki kız sayısı ile erkek sayısı eşit olup bu çözüm ile 28 kişi de yaklaşık olarak eşittir ve tüm kişinin çift olması zorunludur. Yanıtlardan daha açıklayıcı bir sonuç verilemez.
İkinci Bölüm: Kareköklü Sayılar Kartı Sorusu
Soru 16:
Yukarıda üzerinde karekökü ifadelerin yazılı olduğu 6 tane kart verilmiştir. Her kart birer kez kullanılarak, üzerlerindeki sayıların çarpımları bir doğal sayı olacak şekilde ikişerli gruplanacaktır. Buna göre, bu gruplama yapıldığında aşağıdakilerden hangisi dışarıda kalan kartlardan biridir?
Kartlar:
- \sqrt{18}
- \sqrt{12}
- \sqrt{24}
- \sqrt{6}
- \sqrt{20}
- \sqrt{8}
Yanıt:
Kartları ikişerli olarak çarptığımızda, sonucun bir doğal sayı olması için, çarpımların karekök içeriğinin tam kare olması gerekir. Şimdi bunu kontrol edelim:
- (\sqrt{18} \cdot \sqrt{2}) = \sqrt{36} = 6 (doğal sayı)
- (\sqrt{12} \cdot \sqrt{6}) = \sqrt{72} \neq doğal sayı
- (\sqrt{24} \cdot \sqrt{6}) = \sqrt{144} = 12 (doğal sayı)
- (\sqrt{20} \cdot \sqrt{5}) = \sqrt{100} = 10 (doğal sayı)
- (\sqrt{8} \cdot \sqrt{2}) = 4 (doğal sayı)
Burada dışarıda hangi kart kalıyor bu uygun gruplama yaparken:
- \sqrt{12} ve \sqrt{8} gruplandığında \sqrt{96} (bu uygun değil).
Dolayısıyla dışarıda kalan kart B) \sqrt{12} olur.
Matematik sorularında grafik ve köklü sayılar içeren çözümlemeden önce dikkatle çalışmak ve bulguları doğrulamak önemlidir çünkü açı ve çarpanlara dikkat edilerek yapılan işlemler hatalı olabilir.