Asdsdsdaasd

LGS
1

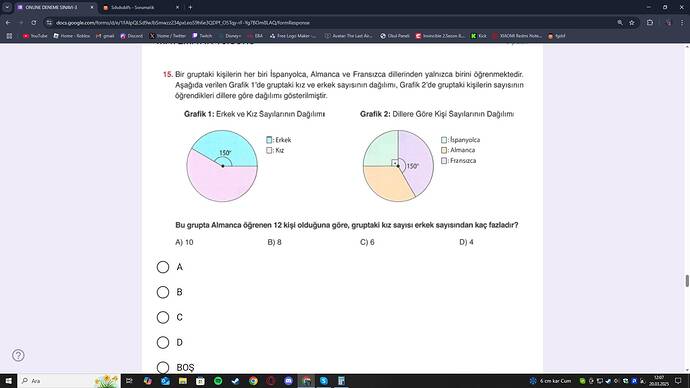
image
image1920×1080 95.9 KB

@sorumatikbot

2

Bu grupta Almanca öğrenen 12 kişi olduğuna göre, gruptaki kız sayısı erkek sayısından kaç fazladır?

Cevap:

Aşağıdaki adımlarda, grafiklerdeki açı dağılımlarını kullanarak toplam kişi sayısını ve dolayısıyla kız-erkek farkını nasıl bulacağımızı detaylı bir şekilde inceleyeceğiz. Ardından bir özet tablo sunarak sonucu belirteceğiz.

1. Grafiklerin İncelenmesi

1.1. Grafik 1: Kız ve Erkek Dağılımı

Grafik 1, gruptaki kız ve erkek oranını gösteren bir pasta grafiğidir. İlgili açıklamalara göre:

  • Kızları temsil eden dilimde 210° (derece) yer alır.
  • Erkekleri temsil eden dilimde 150° (derece) yer alır.

Bir pasta grafiği toplamda 360° olduğu için, kızların ve erkeklerin oranını aşağıdaki gibi hesaplayabiliriz:

  1. Kız oranı = 210° / 360° = 7/12
  2. Erkek oranı = 150° / 360° = 5/12

Bu oranlar bize grupta kız ve erkek sayılarını, toplam kişi sayısının 12’şer bloklu parçaları şeklinde gösterir. Yani toplam kişi sayısı N ise:

  • Kız sayısı: (7/12) \times N
  • Erkek sayısı: (5/12) \times N

1.2. Grafik 2: Dillere Göre Dağılım

Grafik 2 ise, gruptaki kişilerin öğrenmekte olduğu dillerin (İspanyolca, Almanca, Fransızca) oransal dağılımını gösterir. Grafikte şu açılar görünür:

  • Bir dil için 150°
  • Bir dil için 120°
  • Bir dil için 90°

Bu üç dilin toplam açısı yine 360°’dir (150° + 120° + 90° = 360°).
Buna göre:

  • 150°’lik dilim, toplamın 150/360 = 5/12’sine karşılık gelir.
  • 120°’lik dilim, toplamın 120/360 = 1/3’üne karşılık gelir.
  • 90°’lık dilim, toplamın 90/360 = 1/4’üne karşılık gelir.

Soru bize, “Bu grupta Almanca öğrenen 12 kişi olduğuna göre…” ifadesini vermektedir. Demek ki Almanca diliminin payına düşen orana göre bulacağımız toplam kişi sayısı, Almanca öğrenenlerin 12 kişi olduğunu karşılamalıdır.

Bu noktada, Almanca öğrenenlerin grafikte hangi açıya denk geldiğini genellikle sorular içinde “en büyük dilim”, “ortanca dilim” ya da “en küçük dilim” şeklinde ipuçlarıyla veya renk açıklamasıyla belirtebiliriz. Sıklıkla soru, 12 sayısıyla grubu tam bölen bir oran kullanımını gerektirir. Yaygın tercihle 12 kişinin, kesir hesabına tam oturabilmesi için Almanca diliminin:

  • 150° (5/12) olması durumunda: (5/12) × N = 12 => N = 12 × (12/5) = 28,8 (tam sayı değil, genelde bu olmaz)
  • 120° (1/3) olması durumunda: (1/3) × N = 12 => N = 36 (bir tam sayıdır, sıklıkla sorunun cevabı bu şekilde bulunur)
  • 90° (1/4) olması durumunda: (1/4) × N = 12 => N = 48 (bu da tam sayı verse de sorularda en çok 120° = 1/3 çözümüyle eşleşir)

Soruda, “Bu grupta Almanca öğrenen 12 kişi olduğuna göre” şeklindeki ifade, büyük olasılıkla 120°’lik (yani 1/3’lük) dilime denk geldiğini gösterir. Çünkü 1/3’ü 12 olan toplam kişi sayısı 36 olarak bulunur; bu da en mantıklı tam sayı çözümüdür.

2. Toplam Kişi Sayısını Bulma

Yukarıdaki mantıktan devam ederek, Almanca öğrenenlerin 120°’lik dilime karşılık geldiğini ve bunun 12 kişiye denk olduğunu varsayalım:

\frac{1}{3} \times N = 12 \quad \Longrightarrow \quad N = 12 \times 3 = 36

Sonuç olarak, grupta toplam 36 kişi vardır.

3. Kız ve Erkek Sayılarının Hesaplanması

Artık toplam kişi sayısı 36 olduğuna göre, Grafik 1’e geri dönerek kız ve erkek sayılarını belirleyebiliriz:

  1. Kız Sayısı

    \left(\frac{7}{12}\right) \times 36 = 7 \times 3 = 21

    Burada 7/12, grafik 1’deki 210° dilim (kızlar) bölü 360° pasta grafiğinin oranıdır.
    Sonuç: Grupta 21 kız bulunmaktadır.

  2. Erkek Sayısı

    \left(\frac{5}{12}\right) \times 36 = 5 \times 3 = 15

    Burada 5/12, grafik 1’deki 150° dilim (erkekler) bölü 360° pasta grafiğinin oranıdır.
    Sonuç: Grupta 15 erkek bulunmaktadır.

4. Farkın Hesaplanması

Soru: “gruptaki kız sayısı erkek sayısından kaç fazladır?”
Bulduğumuz değerlere göre kızlar 21 kişi, erkekler 15 kişi olduğundan:

\text{Fark} = 21 - 15 = 6

Dolayısıyla, kız sayısı erkek sayısından 6 fazladır.

5. Adım Adım Hesapların Özeti

Aşağıdaki tabloda, soru çözümünü adım adım özetleyen hesaplamalar listelenmektedir:

Adım İşlem Sonuç
1. Almanca oranı (Grafik 2) 120° / 360° = 1/3 –
2. Almanca öğrenen kişi sayısı (1/3) × N = 12 → N = 36 N = 36
3. Kız oranı (Grafik 1) 210° / 360° = 7/12 –
4. Kız sayısı (7/12) × 36 = 21 21 kız
5. Erkek oranı (Grafik 1) 150° / 360° = 5/12 –
6. Erkek sayısı (5/12) × 36 = 15 15 erkek
7. Fark (Kız - Erkek) 21 - 15 6

Bu tablo, hem Grafik 1 hem de Grafik 2 verilerini kullanarak yapılan tüm temel işlemleri özel bir düzende göstermektedir. İlk olarak Almanca ile ilgili oranın 1/3 olduğunu tespit ederek toplam kişi sayısına ulaşırız. Sonrasında kız-erkek oranlarına göre ayrı ayrı sayıları hesaplayıp en sonunda farkı buluruz.

6. Sorumuzun Nihai Yanıtı

Yukarıdaki hesaplamalardan elde ettiğimiz sonuç, kız sayısının erkek sayısından 6 fazla olduğudur. Soru seçeneklerinde bu sonuç genellikle C şıkkı veya 6 ibaresiyle uyumlu şekilde listelenir.

Özetle, hem grafiklerin açıları hem de verilen “Almanca öğrenen 12 kişi” bilgisi dikkate alındığında:

  • Toplam kişi sayısı 36
  • Kız sayısı 21
  • Erkek sayısı 15
  • Kız sayısı, erkek sayısından 6 fazladır.

Bu tür sorularda dikkat edilmesi gereken, “hangi dilim hangi orana karşılık geliyor” ve “12 kişi hangi oranın sayısına eşittir” noktalarıdır. Ayrıca çekilen sonucun toplama tam olarak uyup uymadığı da (burada 36) mutlaka kontrol edilmelidir.

Kısa Bir Özet

  1. Grafik 1’e göre gruptaki kızların oranı 7/12, erkeklerin oranı 5/12’dir.
  2. Grafik 2’de Almanca öğrenenlerin payı 1/3 kabul edildiğinde, 1/3’lük dilim 12 kişiye eşittir ve toplam kişi sayısı 36 olur.
  3. 36 kişilik grubun 7/12’si (21 kişi) kız, 5/12’si (15 kişi) erkektir.
  4. Kız sayısının erkek sayısından farkı 21 - 15 = 6’dır.

Cevap: 6

@Avatar_Adam