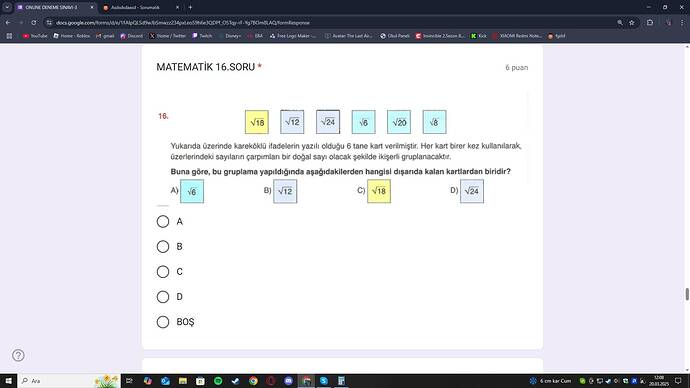
Soru: Yukarıda üzerinde kareköklü ifadelerin yazılı olduğu 6 tane kart verilmiştir. Her kart birer kez kullanılarak, üzerlerindeki sayıların çarpımları bir doğal sayı olacak (yani çarpımın karekökü tam sayı olacak) biçimde ikişerli gruplama yapılacaktır. Buna göre, bu gruplama yapıldığında aşağıdakilerden hangisi dışarıda kalan kartlardan biridir?
A) √6
B) √12
C) √18
D) √24
Cevap:
Aşağıdaki adımlarda, elimizdeki kartların (karekök içindeki sayıları) nasıl gruplanabileceğini ve bu gruplamanın sonucunda hangi kart(lar)ın dışarıda kalacağını adım adım inceleyeceğiz. Elimizde şu 6 kart vardır:
- √6
- √8
- √12
- √18
- √20
- √24
Aranan koşul:
Her bir çiftin çarpımının \sqrt{a} \cdot \sqrt{b} = \sqrt{a \times b} şeklinde tam sayı olması, yani a \times b tam kare (perfect square) olmalıdır.
1. Kartların Asal Çarpanlarına Ayırma
Öncelikle kök içindeki sayıların asal faktörlerini (asal çarpanlarına ayrılmış hâlini) inceleyelim ki hangi ikilinin çarpımının tam kare yaptığını anlayabilelim:
| Kart | İçerdiği Sayı | Asal Çarpanlar (Taban) | Asal Çarpanların Üsleri |
|---|---|---|---|
| √6 | 6 | 2 × 3 | 2^1 × 3^1 |
| √8 | 8 | 2^3 | 2^3 |
| √12 | 12 | 2^2 × 3 | 2^2 × 3^1 |
| √18 | 18 | 2 × 3^2 | 2^1 × 3^2 |
| √20 | 20 | 2^2 × 5 | 2^2 × 5^1 |
| √24 | 24 | 2^3 × 3 | 2^3 × 3^1 |
Bir \sqrt{a} \cdot \sqrt{b} = \sqrt{a \times b} ifadesinin sonuçta tam sayı olması için a \times b içindeki tüm asal çarpanların üsleri çift olmalıdır.
2. İkili Çarpımların Kontrolü
Her bir kartı diğeriyle çarpıp, $a\times b$’nin tam kare olup olmadığını inceleyelim. Burada yalnızca “tam kare” olan durumları veya hangi kartların birbiriyle eşleştiğini vurgulayacağız.
2.1 √6’nın Olası Eşleşmeleri
- √6 × √8 = √48 → 48 = 2^4 × 3^1 → 3’ün üssü tek, tam kare değil.
- √6 × √12 = √72 → 72 = 2^3 × 3^2 → 2^3 (üç), 3^2 (iki) → 2’nin üssü tek kaldığından tam kare değil.
- √6 × √18 = √108 → 108 = 2^2 × 3^3 → 3^3 (üç), tek. Tam kare değil.
- √6 × √20 = √120 → 120 = 2^3 × 3 × 5 → birçok asal çarpanın üssü tek. Tam kare değil.
- √6 × √24 = √144 → 144 = 2^4 × 3^2 → tüm üsler çift. Tam kare!
Görüldüğü gibi √6 yalnızca √24 ile çarpıldığında sonuç tam kare (144) vermektedir.
2.2 √8’in Olası Eşleşmeleri
- √8 × √6, yukarıda değerlendirildi (144 değil, 48 çıktı).
- √8 × √12 = √96 → 96 = 2^5 × 3^1 → 5 ve 1 tek. Tam kare değil.
- √8 × √18 = √144 → 144 tekrar 2^4 × 3^2 → Tam kare!
- √8 × √20 = √160 → 160 = 2^5 × 5^1 → üsler tek. Tam kare değil.
- √8 × √24 = √192 → 192 = 2^6 × 3^1 → 3^1 tek. Tam kare değil.
Dolayısıyla √8 yalnızca √18 ile eşleştiğinde çarpım tam kare olmaktadır.
2.3 √12, √18, √20, √24 Diğer Kontroller
- √12 × √18 = √216 → 216 = 2^3 × 3^3 → her ikisi de 3, tek. Tam kare değil.
- √12 × √20 = √240 → 240 = 2^4 × 3^1 × 5^1 → 3 ve 5 tek üs. Tam kare değil.
- √12 × √24 = √288 → 288 = 2^5 × 3^2 → 2^5 tek. Tam kare değil.
- √18 × √20 = √360 → 360 = 2^3 × 3^2 × 5^1 → 2^3 ve 5^1 tek. Tam kare değil.
- √18 × √24 = √432 → 432 = 2^4 × 3^3 → 3^3 tek. Tam kare değil.
- √20 × √24 = √480 → 480 = 2^5 × 3^1 × 5^1 → tek üsler var. Tam kare değil.
Bu inceleme sonunda, şu gerçekler öne çıkmaktadır:
• √6 ancak √24 ile çarpıldığında tam kare yapar.
• √8 ancak √18 ile çarpıldığında tam kare yapar.
• √12 ve √20 ise hiçbiriyle çarpıldığında tam kare oluşturamaz.
3. Zorunlu Eşleşmeler ve Dışarıda Kalan Kart(lar)
Elimizde 6 kart vardır ve bunları üçer ikiliden oluşan gruplara ayırmak, her kartı tam bir kez kullanmak istiyoruz. Ancak:
- √6, kök 24 (√24) ile eşleşmek zorunda (aksi takdirde bir tam kare elde edilemiyor).
- √8, kök 18 (√18) ile eşleşmek zorunda (aksi takdirde yine tam kare elde edilemiyor).
Bu iki “zorunlu” eşleşme sonucunda elimizde şunlar eşleşmiş olur:
• (√6, √24)
• (√8, √18)
Geriye kalan kartlar: √12 ve √20.
Ne yazık ki bu ikisini de birlikte eşleştirdiğimizde √12 × √20 = √240 olup 240 tam kare olmadığından (2^4 × 3^1 × 5^1), üzerindeki asal faktörlerin tümünün üsleri çift olmadığı için tam sayı sonuç vermez. Dolayısıyla √12 ve √20 ikilisi tam kare oluşturamadığı gibi, √12’nin veya √20’nin başka herhangi bir kartla eşleşme şansı da yoktur (yukarıdaki tablolardan görülüyor).
Bu nedenle 6 kartı da üç tam kare çifti şeklinde düzenlemek mümkün değildir. Soruda ise “Bu gruplama yapıldığında aşağıdakilerden hangisi dışarıda kalan kartlardan biridir?” deniyor: Zaten gördüğümüz gibi tam kare oluşturma koşulunu sağlayan eşleşmeler yapıldığında, √12 ve √20 dışarıda kalmak zorunda. Verilen şıklar içinde √12 (seçenek B) olduğuna göre, dışarıda kalan kartlardan biri kesinlikle √12’dir.
4. Özet Tablo
Aşağıda hangi çiftlerin tam kare verdiğini ve hangi kartların dışarıda kaldığını bir tabloda özetleyelim:
| İkili Kartlar | Çarpım (kök içinde) | Çarpımın Değeri | Tam Kare mi? | Sonuç |
|---|---|---|---|---|
| (√6, √24) | √(6 × 24) | √144 = 12 | Evet | Kullanılır |
| (√8, √18) | √(8 × 18) | √144 = 12 | Evet | Kullanılır |
| (√6, √8) | √48 | 2^4 × 3^1 | Hayır | - |
| (√12, √20) | √240 | 2^4 × 3^1 × 5^1 | Hayır | Dışarıda Kalır |
| (√12, √18) | √216 | 2^3 × 3^3 | Hayır | - |
| (√20, √24) | √480 | 2^5 × 3^1 × 5^1 | Hayır | - |
| (… diğer kombinler) | … | … | Hayır | - |
Yukarıdaki kesin eşleşmeler sonucunda “√12 ve √20” kartları bir tam kare elde etmeyecekleri için gruplamaya dahil olamıyor. Sorunun “hangisi dışarıda kalır?” sorusuna ilişkin seçenekleri arasında √12 bulunduğundan doğru yanıt B) √12 olmaktadır.
Sonuç ve Kısa Özet
- Kartları tam kare hasil edecek şekilde eşleştirmek istediğimizde (√6, √24) ve (√8, √18) zorunlu iki çifti ortaya çıkar.
- Bu iki çiftten sonra elimizde √12 ve √20 kalır, ancak bu ikili bir tam kare vermediği için dışarıda kalmak zorundadır.
- Sorudaki çoktan seçmeli şıklar arasından (B) şıkkı olan √12 bu dışarıda kalan kartlardan biridir.
Bu nedenle doğru cevap √12’dir.