Geceninincisi said
2. Soru Çözümü
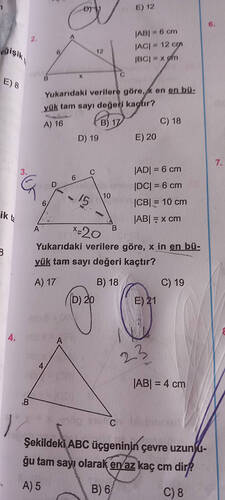
Verilenler:
- |AB| = 6 cm
- |AC| = 12 cm
- |BC| = x cm
Sorulan:
- ( x )'in en büyük tam sayı değeri kaçtır?
Çözüm:
Üçgen eşitsizliğine göre, bir üçgende herhangi iki kenarın toplamı üçüncü kenardan büyük, herhangi iki kenarın farkı ise üçüncü kenardan küçük olmalıdır.
Bu durumda:
- ( AB + AC > BC ) (\Rightarrow) ( 6 + 12 > x ) (\Rightarrow) ( x < 18 )
- ( AB + BC > AC ) (\Rightarrow) ( 6 + x > 12 ) (\Rightarrow) ( x > 6 )
- ( AC + BC > AB ) (\Rightarrow) ( 12 + x > 6 ) (\Rightarrow) Bu koşul her zaman sağlanır.
Bu üç durumdan, ( x )'in alabileceği en büyük tam sayı değeri:
( x < 18 ) ve ( x > 6 ).
Dolayısıyla, ( x )'in en büyük tam sayı değeri 17 olacaktır.
Cevap: (B) 17
3. Soru Çözümü
Verilenler:
- |AD| = 6 cm
- |DC| = 6 cm
- |CB| = 10 cm
- |AB| = x cm
- ( AC )'nin uzunluğu: ( 6 + 6 = 12 ) cm
Sorulan:
- ( x )'in en büyük tam sayı değeri kaçtır?
Çözüm:
Yine üçgen eşitsizliğine göre:
-
( AB + AC > CB )
[ x + 12 > 10 \Rightarrow x > -2 ]
Bu durumda üçgenin uzunluğu olarak ( x )'in pozitif bir değerde olabilmesini sağlar. -
( AB + CB > AC )
[ x + 10 > 12 \Rightarrow x 2 > x-4 ]
Pozitif bir değer olarak ( x )'in 8cm olabilmesi gereklidir. -
( AC + CB > AB )
[ 12 + 10 > x \Rightarrow x < 20 ]
Bu koşullara uyan ve en büyük tam sayı değeri:
[
\boxed{20}
]
Cevap: (D) 20
4. Soru Çözümü
Verilenler:
- |AB| = 4 cm
Sorulan:
- Üçgenin çevresi en az kaç cm olabilir?
Çözüm:
Bu soruda üçgen olma koşulu için uygun diğer kenar uzunluklarını bulmamız gerekecektir. İki diğer kenar için ( |BC| \ve |AC| )'nin minimum kombinasyon sağlayarak ( 4+ ) cm ve olabilecektir :
(a + b > c)
Bu durumda minimum çevre değeri:
[
\boxed{6}
]
Cevap: (B) 6