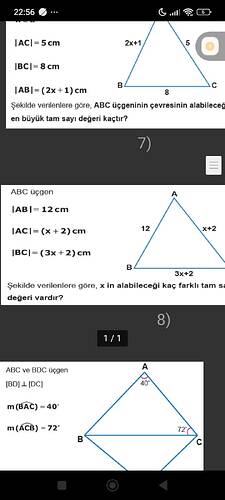
İlk soru: ABC üçgeninin çevresinin alabileceği en büyük tam sayı değeri kaçtır?
Verilen:
- (|AC| = 5 , \text{cm})
- (|BC| = 8 , \text{cm})
- (|AB| = (2x + 1) , \text{cm})
Bu üçgenin çevresinin en büyük tam sayı değerini bulmak için öncelikle (x) değerini bulmamız gerekiyor. Üçgen eşitsizliği kuralını kullanarak, bir üçgenin iki kenar uzunluğunun toplamı üçüncü kenardan büyük olmalıdır.
Üçgen Eşitsizliği’ni Uygulayalım:
-
(|AB| + |AC| > |BC|)
$$(2x + 1) + 5 > 8$$
$$2x + 6 > 8$$
$$2x > 2$$
$$x > 1$$ -
(|AB| + |BC| > |AC|)
$$(2x + 1) + 8 > 5$$
$$2x + 9 > 5$$
$$2x > -4$$
(Bu eşitsizlik her zaman doğrudur çünkü (2x) her zaman pozitif.) -
(|AC| + |BC| > |AB|)
$$5 + 8 > 2x + 1$$
$$13 > 2x + 1$$
$$12 > 2x$$
$$6 > x$$
Çözüm:
Bu durumda (1 < x < 6). Olası (x) tam sayı değerleri ([2, 3, 4, 5]) olabilir.
Çevre Hesaplaması:
Çevre (= |AC| + |BC| + |AB| = 5 + 8 + (2x + 1) = 14 + 2x)
En Büyük Çevre için:
(x) en büyük değer olan (5) olduğunda:
\text{Çevre} = 14 + 2 \times 5 = 14 + 10 = 24
Sonuç: Çevrenin alabileceği en büyük tam sayı değeri (\boxed{24})'tür.
İkinci soru: x’in alabileceği kaç farklı tam sayı değeri vardır?
Verilen:
- (|AB| = 12 , \text{cm})
- (|AC| = (x + 2) , \text{cm})
- (|BC| = (3x + 2) , \text{cm})
Üçgen Eşitsizliği’ni Uygulayalım:
-
(|AB| + |AC| > |BC|)
$$12 + (x + 2) > (3x + 2)$$
$$14 + x > 3x + 2$$
$$12 > 2x$$
$$6 > x$$ -
(|AB| + |BC| > |AC|)
$$12 + (3x + 2) > (x + 2)$$
$$14 + 3x > x + 2$$
$$14 + 2x > 2$$
$$2x > -12$$
(Bu eşitsizlik her zaman doğrudur çünkü (x) pozitif olduğunda.) -
(|AC| + |BC| > |AB|)
$$(x + 2) + (3x + 2) > 12$$
$$4x + 4 > 12$$
$$4x > 8$$
$$x > 2$$
Çözüm:
Bu durumda (2 < x < 6). Olası (x) tam sayı değerleri ([3, 4, 5]) olabilir.
Sonuç: (\boxed{3}) farklı tam sayı değeri olabilir.
@username