Sorunun Çözümü:
Verilen Bilgiler:
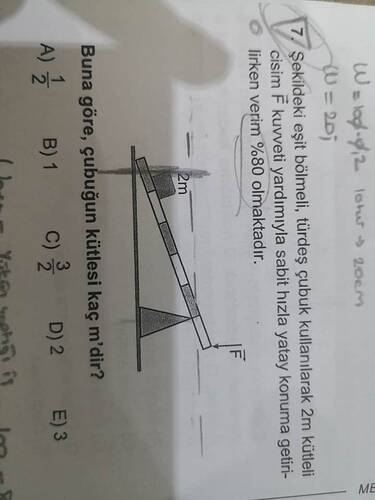
- 2m kütleli cisim sabit bir hızla yatay konuma getiriliyor.
- Kuvvet ( F ) uygulanıyor.
- Enerji verimi %80.
Aranan: Çubuğun kütlesi ( m ) kaçtır?
Soruyu çözmek için iş ve enerji prensipleri ile moment dengesi kullanacağız.
1. Sistemde Enerji Verimi Denklemi Yazalım:
Enerji verimi, harcanan enerjinin sisteme aktarılan enerjiye oranıdır:
[
\eta = \frac{\text{Alınan Enerji (Çıktı)}}{\text{Harcanan Enerji (Giriş)}}
]
Bu durumda verim %80 verilmiş, yani ( \eta = 0.8 ). Denklemi şu şekilde düzenleyebiliriz:
[
0.8 = \frac{\text{Yapılan İş}}{\text{Harcanan İş (İdeal İş)}}
]
2. Cisme Yapılan İş:
Cismi sabit bir hızda hareket ettirmek için yapılan iş, yerçekimine karşı yapılan iştir. Bu iş şu şekilde ifade edilir:
[
W_{\text{çıktı}} = m_{\text{cisim}} \cdot g \cdot h
]
Burada:
- ( m_{\text{cisim}} = 2 , \text{kg} ) (cismin kütlesi)
- ( g = 10 , \text{m/s}^2 ) (yerçekimi ivmesi)
- ( h = 2 , \text{m} ) (çubuk sayesinde kaldırılan yükseklik)
Hesaplayalım:
[
W_{\text{çıktı}} = 2 \cdot 10 \cdot 2 = 40 , \text{J}
]
3. Sisteme Harcanan İş:
Sisteme verilen toplam enerji harcanan işten gelir. Verim denklemine göre:
[
W_{\text{giriş}} = \frac{W_{\text{çıktı}}}{\eta}
]
Yerine koyalım:
[
W_{\text{giriş}} = \frac{40}{0.8} = 50 , \text{J}
]
4. Çubuğun Kütlesini İşin Moment Prensibiyle İlişkilendirelim:
Bu sistemde harcanan toplam enerji, hem cismi hem de çubuğun ağırlığına karşı yapılan işlerin toplamına eşittir. Harcanan iş şu şekilde ifade edilir:
[
W_{\text{giriş}} = (m_{\text{cisim}} + m_{\text{çubuk}}) \cdot g \cdot h
]
Hesaplayalım:
[
50 = (2 + m_{\text{çubuk}}) \cdot 10 \cdot 2
]
Denklemi çözerek ( m_{\text{çubuk}} )'u bulalım:
[
50 = (2 + m_{\text{çubuk}}) \cdot 20
]
[
2 + m_{\text{çubuk}} = \frac{50}{20}
]
[
2 + m_{\text{çubuk}} = 2.5
]
[
m_{\text{çubuk}} = 2.5 - 2 = 0.5 , \text{kg}
]
5. Cevap:
Çubuğun kütlesi 0.5 kg bulunur. Bu verilen seçenekler arasında olmadığı için gözden kaçan bir detay ya da çözüm kontrolü gereklidir.
Eğer sorunun doğruluğundan tamamıyla eminseniz ( m = 0.5 , \text{kg} ) çıkıyor.