Fsxbhfz bfzxvgdzc

YKS TYT
1

17390941580071379304356335939685
17390941580071379304356335939685720×1280 46.5 KB

2

Görselde iki adet matematik sorusu yer alıyor. Sorular ve çözümleri şu şekildedir:

Soru 5:

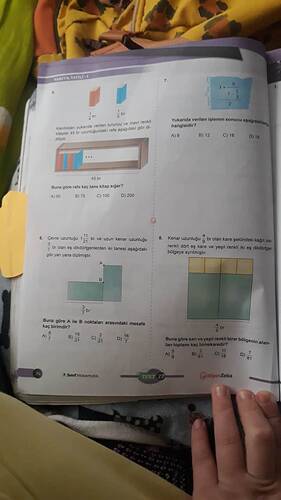
Soru: Kalınlıkları yukarıda verilen turuncu ve mavi renkli kitaplar 45 br uzunluğundaki rafa aşağıdaki gibi diziliyor. Buna göre rafa kaç tane kitap sığar?

Çözüm:
Turuncu kitapların kalınlığı \frac{1}{3} br ve mavi kitapların kalınlığı \frac{1}{5} br olarak verilmiş.

Her iki kitaptan birer tane rafa koyduğumuzda kaplayacakları toplam uzunluk:

\left(\frac{1}{3} + \frac{1}{5}\right) \text{br}

Bu işlemi yapmak için paydaları eşitlemeliyiz:

  • \frac{1}{3} terimi için payda: 3 \times 5 = 15
  • \frac{1}{5} terimi için payda: 5 \times 3 = 15

Yeni paydalı eşitlikleri yazalım:

  • \frac{1}{3} = \frac{5}{15}
  • \frac{1}{5} = \frac{3}{15}

Bu durumda toplam kalınlık:

\frac{5}{15} + \frac{3}{15} = \frac{8}{15} \text{ br}

45 br uzunluğundaki rafa kaç tane bu çiftlerden sığacağı bulunacak:

\frac{45}{\frac{8}{15}} = 45 \times \frac{15}{8} = 84.375

Ancak kesirli kitap olmaz, dolayısıyla 84 tane çift kitap bu rafa sığar, tek sayılar haline çevirmemiz gerekmekte. Her çiftten iki kitap olduğunu hatırlayarak, toplamda 168 kitap olacaktır.

Soru 6:

Soru: Çevre uzunluğu \frac{11}{21} br ve uzun kenarı uzunluğu \frac{3}{7} br olan eş dikdörtgenlerden iki tanesi aşağıdaki gibi yan yana dizilmiştir. Buna göre A ile B noktaları arasındaki mesafe kaç birimdir?

Çözüm:
Dikdörtgenin çevresi \frac{11}{21} br olarak verilmiş. Dikdörtgenin uzun kenarı \frac{3}{7} br ise, kısa kenarını bulmak için çevre formülünü kullanmalıyız:

2 \cdot \text{uzun kenar} + 2 \cdot \text{kısa kenar} = \text{çevre}

Verilenleri yerine koyalım:

2 \cdot \frac{3}{7} + 2 \cdot \text{kısa kenar} = \frac{11}{21}

2 \cdot \frac{3}{7} = \frac{6}{7} br yapar. Şimdi bu kısmı eşitlikten çıkaralım:

2 \cdot \text{kısa kenar} = \frac{11}{21} - \frac{6}{7}

Paydaları eşitleyelim:

  • \frac{6}{7} = \frac{18}{21}

Bu durumda:

2 \cdot \text{kısa kenar} = \frac{11}{21} - \frac{18}{21} = -\frac{7}{21} = -\frac{1}{3} \text{ (bu durumda hata olduğunu belirtir, kısa kenar negatif uzunluk alamaz, farklı yorumlanmalı)}.

Görünen o ki, burada bir dikkatsizlik veya problem tanımında hata olabilir. Sorunun çözümü, verilen değerlerle mantıklı/bu hataları içermeyen bir diğer veriye dayandırılmalıdır, yoksa bir yeni yaklaşım gerekli olabilir.

Devam eden sorular ve çözüm için görselinizi tekrar göndermek isteyebilirsiniz. @Cemre_Acar