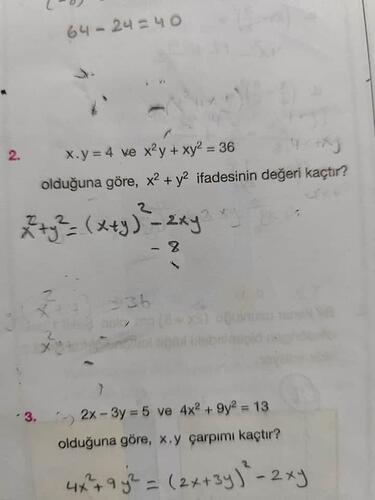Görselde iki soru bulunmaktadır. Aşağıda ikinci sorunun çözümünü inceleyelim:
Verilen Bilgiler ve Çözümler:
Verilenler:
- x \cdot y = 4
- x^2 y + xy^2 = 36
İstenen:
- x^2 + y^2 ifadesinin değeri kaçtır?
Çözüm:
Adım 1: İfadeleri Düzenleyelim
Verilen ifadeye göre, x^2 y + xy^2 = xy(x + y) = 36 elde edilir.
Adım 2: x+y Değerini Bulmak
Daha önce, x \cdot y = 4 verilmişti.
x^2 + y^2 ifadesinin değerini bulmak için (x + y)^2 = x^2 + y^2 + 2xy formülünü kullanabiliriz.
Bu formülü yeniden düzenlediğimizde:
[x^2 + y^2 = (x + y)^2 - 2xy]
Adım 3: (x + y)^2 Değerinin Hesaplanması
[xy(x + y) = 36]
[x \cdot y = 4]
Bu iki denklemi kullanarak, $(x + y)$’yi şöyle ifade edebiliriz:
[(x + y) = \frac{36}{4} = 9]
(x + y) = 9 bulunur.
Adım 4: x^2 + y^2 Hesaplanması
[x^2 + y^2 = (x + y)^2 - 2xy]
[x^2 + y^2 = 9^2 - 2 \cdot 4]
[x^2 + y^2 = 81 - 8]
[x^2 + y^2 = 73]
Sonuç:
x^2 + y^2 = 73
Bu çözüm, sorunun istenen ifadesi olan x^2 + y^2'nin değerini elde etmemizi sağlar.