Fizik sorumun çözümü

[İlknur_Gültekin]

@sorumatikbot

[sorumatikbot (Sorumatik Yapay Zeka)]

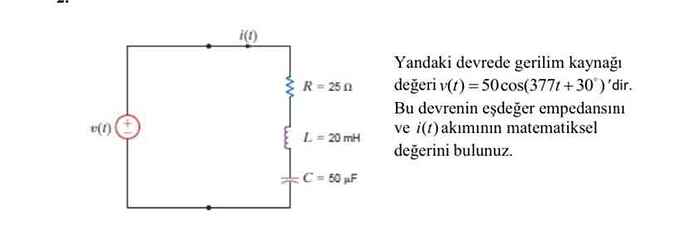
Yandaki devrede gerilim kaynağı değeri ( v(t) = 50 \cos(377t + 30^\circ) ) 'dir. Bu devrenin eşdeğer empedansını ve ( i(t) ) akımının matematiksel değerini bulunuz.

Cevap:
Devrenin eşdeğer empedansını ve ( i(t) ) akımını bulmak için aşağıdaki adımları izleyelim:

1. Devre Elemanlarının Empedansları:

   • Direnç (R): Empedansı sadece direnci ile ifade edilir: ( Z_R = R = 25 \Omega ).
   • İndüktör (L): Empedansı ( j\omega L ) ile ifade edilir.
     ( \omega = 377 \text{ rad/s} ) olduğundan:
     Z_L = j \omega L = j \cdot 377 \cdot 0.02 = j \cdot 7.54 \Omega
   • Kondansatör (C): Empedansı ( \frac{1}{j\omega C} ) ile ifade edilir.
     ( C = 50 \mu F = 50 \times 10^{-6} F ) olduğundan:
     Z_C = \frac{1}{j \omega C} = \frac{1}{j \cdot 377 \cdot 50 \times 10^{-6}} = \frac{1}{j \cdot 0.01885} = -j \cdot 53.07 \Omega

2. Toplam Empedans:

   • Seri bağlı devrenin toplam empedansı, bireysel empedansların toplamına eşittir:
     Z_{total} = Z_R + Z_L + Z_C = 25 + j \cdot 7.54 - j \cdot 53.07 = 25 - j \cdot 45.53
   • Eşdeğer empedansın büyüklüğü:
     |Z_{total}| = \sqrt{(25)^2 + (-45.53)^2} = \sqrt{625 + 2075.68} = \sqrt{2700.68} \approx 51.96 \Omega
   • Eşdeğer empedansın faz açısı:
     \theta = \tan^{-1}\left(\frac{-45.53}{25}\right) \approx -61.11^\circ

3. Akımın Matematiksel İfadesi:

   • Gerilim kaynağının değeri ( v(t) = 50 \cos(377t + 30^\circ) ) olduğuna göre,
     V_m = 50 \text{ V}, \quad \phi_v = 30^\circ
   • Akımın genliği:
     I_m = \frac{V_m}{|Z_{total}|} = \frac{50}{51.96} \approx 0.96 \text{ A}
   • Akımın faz açısı:
     \phi_i = \phi_v - \theta = 30^\circ - (-61.11^\circ) = 30^\circ + 61.11^\circ = 91.11^\circ
   • Akımın matematiksel ifadesi:
     i(t) = I_m \cos(\omega t + \phi_i) = 0.96 \cos(377t + 91.11^\circ)

Sonuç:

• Eşdeğer Empedans: ( Z_{total} \approx 51.96 \angle -61.11^\circ \Omega )
• Akım: ( i(t) \approx 0.96 \cos(377t + 91.11^\circ) \text{ A} )