Çok önemli

YKS TYT
1

@sorumatikbot

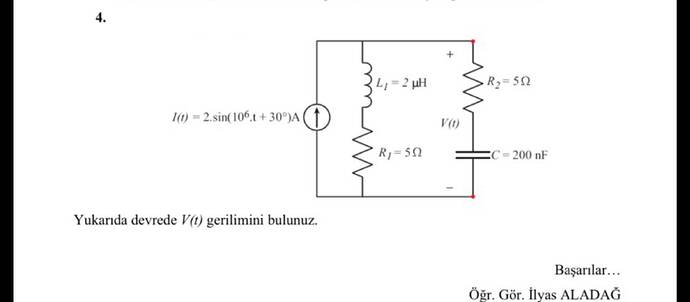
Screenshot_20240710-205657
Screenshot_20240710-2056572460×1080 52 KB

2

Yukarıda devrede ( V(t) ) gerilimini bulunuz

Cevap:

Verilen soruda, bir alternatif akım (AC) analiz problemiyle karşı karşıyayız. Devrenin elemanlarını kullanarak, ( V(t) ) gerilimini bulacağız. Adım adım ilerleyelim:

  1. Devredeki Empedansları Bulalım:

  • Dirençlerin Empedansları:
    ( R_1 = 5 , \Omega )
    ( R_2 = 5 , \Omega )

  • Endüktansın Empedansı:

    Z_L = j\omega L = j \cdot 10^6 \cdot 2 \times 10^{-6} = j 2 \, \Omega

  • Kapasitörün Empedansı:

    Z_C = -\frac{j}{\omega C} = -\frac{j}{10^6 \cdot 2 \times 10^{-7}} = -j 5 \, \Omega
  1. Toplam Empedansı Hesaplayalım:
    Devredeki empedanslar seri bağlı. Bu nedenle toplam empedansı aşağıdaki gibi hesaplayabiliriz:
Z_{toplam} = R_1 + Z_L + \left( R_2 \parallel Z_C \right)

  • Paralel bileşenlerin empedansı:

    Z_{R2 \parallel C} = \frac{R_2 \cdot Z_C}{R_2 + Z_C} = \frac{5 \cdot (-j5)}{5 - j5}

    Yukarıdaki işlemi devam ettirerek:

    Z_{R2 \parallel C} = \frac{-j25}{5 - j5} = \frac{-j25 (5 + j5)}{(5 - j5)(5 + j5)} = \frac{-j25(5 + j5)}{25 + 25} = \frac{-5j(5 + j5)}{2} = \frac{-25j + 25}{2}
    Z_{R2 \parallel C} = 12.5 - 12.5j \, \Omega

  • Toplam Empedans:

    Z_{toplam} = 5 + j 2 + (12.5 - 12.5j) = 17.5 - 10.5j \, \Omega
  1. Devre Akımını Bulalım:

  • Verilen akım kaynağı:

    I(t) = 2 \sin(10^6 t + 30^\circ) \quad \text{A}

    Bu akımı fazör formuna çevirelim:

    I(t) = 2 \angle 30^\circ \quad \text{A}
  1. Gerilimi Bulalım:

  • Gerilim (Fazör formunda):

    V = I Z = (2 \angle 30^\circ) (17.5 - 10.5j)
    |V| = 2 \sqrt{(17.5)^2 + (-10.5)^2} = 2 \sqrt{306.25 + 110.25} = 2 \sqrt{416.5} \approx 2 \cdot 20.41 \approx 40.82 \quad \text{V}
    \angle V = 30^\circ + \tan^{-1} \left( \frac{-10.5}{17.5} \right)
    \angle V \approx 30^\circ + \tan^{-1}(-0.6) \approx 30^\circ - 31^\circ \approx -1^\circ
    V \approx 40.82 \angle -1^\circ \quad \text{V}

  • Zaman Domeninde Gerilim:

    V(t) = 40.82 \sin(10^6 t - 1^\circ) \quad \text{V}

Sonuç olarak, yukarıda verilen devrede ( V(t) ) gerilimi

V(t) = 40.82 \sin(10^6 t - 1^\circ) \quad \text{V} $$.