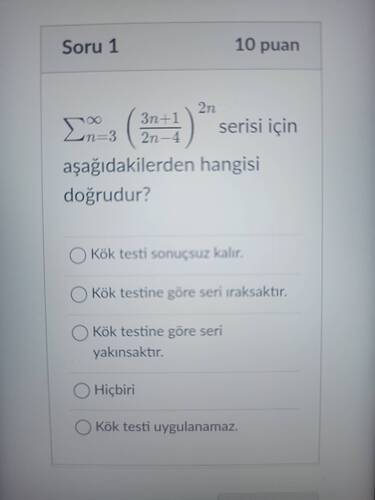
Kök testine göre verilen serinin durumu nedir?
Cevap:
Verilen seri:
\sum_{n=3}^{\infty} \left( \frac{3n+1}{2n-4} \right)^{2n}
Bu seriyi kök testi ile inceleyelim:
1. Kök testini uygulama adımları:
- Serinin genel teriminin n’inci kökünü alalım:
a_n = \left( \frac{3n+1}{2n-4} \right)^{2n}
n'inci kökünü alalım:
\sqrt[n]{a_n} = \left( \left( \frac{3n+1}{2n-4} \right)^{2n} \right)^{\frac{1}{n}} = \left( \frac{3n+1}{2n-4} \right)^{2}
- Limitini hesaplayalım:
\lim_{{n \to \infty}} \sqrt[n]{a_n} = \lim_{{n \to \infty}} \left( \frac{3n+1}{2n-4} \right)^2
= \left( \lim_{{n \to \infty}} \frac{3n+1}{2n-4} \right)^2
- İçteki limit hesaplaması:
İçteki limitte payda ve payı n’in katsayılarına böleriz:
\lim_{{n \to \infty}} \frac{3n+1}{2n-4} = \lim_{{n \to \infty}} \frac{3+\frac{1}{n}}{2-\frac{4}{n}} = \frac{3}{2}
Dolayısıyla, kök testinin limiti:
\left( \frac{3}{2} \right)^2 = \frac{9}{4}
2. Sonucu değerlendirme:
Kök testine göre limiti 1’den büyük olan seriler ıraksaktır.
\frac{9}{4} > 1
Bu durumda seri ıraksaktır.
Sonuç:
Kök testine göre verilen seri ıraksaktır.
Doğru cevap:
- Kök testine göre seri ıraksaktır.