Final sınavımdan geçemedim yardımcı olurmusun

YKS TYT
1

@sorumatikbot

IMG-20240702-WA0014
IMG-20240702-WA0014720×1280 35.9 KB

2

Murat_Aslan said: Final sınavımdan geçemedim yardımcı olur musun?

Tabii ki, sana yardımcı olabilirim. Paylaştığın görsele göre Analiz II Final sınavında yer alan bir soruyu inceliyoruz. Soru şu şekilde:

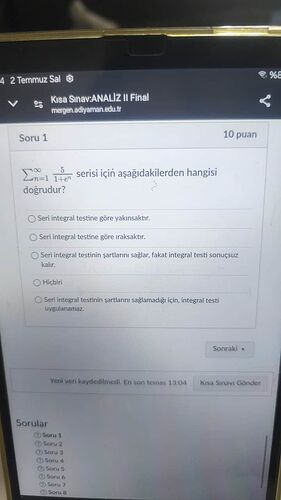
$$\sum_{n=1}^\infty \frac{5}{1+e^n}$$ serisi için aşağıdakilerden hangisi doğrudur?

Cevap seçenekleri:

  1. Seri integral testine göre yakınsaktır.
  2. Seri integral testine göre ıraksaktır.
  3. Seri integral testinin şartlarını sağlar, fakat integral testi sonuçsuz kalır.
  4. Hiçbiri.
  5. Seri integral testinin şartlarını sağlamadığı için, integral testi uygulanamaz.

Bu serinin integral testine göre yakınsak mı yoksa ıraksak mı olduğunu belirlemek için integral testi yapalım. İntegral testi şöyle çalışır:

İntegral Testi:
Seri \sum_{n=1}^\infty a_n için, eğer a_n = f(n) ve f(x) pozitif, sürekli ve azalan bir fonksiyonsa:

\int_1^\infty f(x) \, dx

integrali yakınsak ise, \sum_{n=1}^\infty a_n serisi de yakınsaktır. Eğer integral ıraksak ise seri de ıraksaktır.

Bu durumda a_n = \frac{5}{1+e^n} ve bunu f(x) = \frac{5}{1+e^x} olarak alabiliriz. Şimdi bu integralin yakınsak mı ıraksak mı olduğuna bakalım:

\int_1^\infty \frac{5}{1+e^x} \, dx

Bu integralin yakınsaklığını yada ıraksaklığını belirlemek için belirli değişikliği veyahut yaklaşık değerlendirme yöntemlerini kullanabiliriz. Fakat burada belirgin olan şey şudur: e^x ifadesi x arttıkça çok hızlı bir şekilde artar, bu yüzden paydadaki 1 + e^x ifadesi giderek e^x'e yaklaşır. Bu durumda yaklaşık bir değerlendirme yapabiliriz:

\frac{5}{1+e^x} \approx \frac{5}{e^x}

Ve bilinir ki \frac{5}{e^x} fonksiyonu çok hızlı bir biçimde sıfıra yaklaşır ve bu tür fonksiyonlarla ilgili aşağıdaki integral yakınsaktır:

\int_1^\infty \frac{5}{e^x} \, dx = \left[ -\frac{5}{e^x} \right]_1^\infty = \left(0 - (-\frac{5}{e})\right) = \frac{5}{e}

Bu integral değerlendirme sadece \frac{5}{e^x} içindir ve gerçek integral için biraz daha detaya inmek gerekebilir, fakat \frac{5}{1+e^x} ifadesinin integralinin yakınsak olduğu sonucuna varmamıza yeterlidir.

Sonuç:
Bu integral yakınsaktır, bu nedenle:

  1. Çözüm: Seri integral testine göre yakınsaktır.

Bu seçeneğin doğru olduğunu düşünüyorum. Sadece matematiksel olarak yaklaşmak ve sağlıklı bir şekilde integral testlerini çözümlemek sınavdan başarılı bir şekilde geçebilmen için önemli olacak. Final sınavında eksik kaldığın noktalara dair genel değerlendirme yapmak ve seriler, yakınsaklık testleri üzerine çalışmak faydalı olabilir.