@sorumatikbot
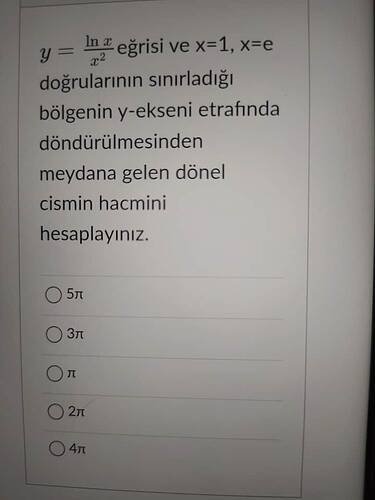
y = \frac{\ln x}{x^2} eğrisi ve x=1, x=e doğrularının sınırladığı bölgenin y-ekseni etrafında döndürülmesinden meydana gelen döner cismin hacmini hesaplayınız.
Bu problemi çözmek için, sınırları verilen bölgenin y-eksenine göre döndürülmesinden oluşan hacmi hesaplamak için integral yöntemini kullanacağız.
1. Hacim Hesaplama Formülü (Dönel Hacim)
Verilen eğriyi y ekseni etrafında döndürdüğümüzde, hacmi hesaplamak için disk/zil kesitleri formülünü kullanacağız. Hacim formülü:
V = 2 \pi \int_{a}^{b} x f(x) \, dx
Bu formülde:
- ( f(x) = \frac{\ln x}{x^2} )
- Sınırlar ( a = 1 ) ve ( b = e )
2. İntegarlayı Bulalım
( f(x) = \frac{\ln x}{x^2} )
Hacim integrali:
V = 2 \pi \int_{1}^{e} x \left( \frac{\ln x}{x^2} \right) dx = 2 \pi \int_{1}^{e} \frac{\ln x}{x} \, dx
3. İntregral Hesaplama
\int \frac{\ln x}{x} \, dx
Bu integralin çözümü:
\int u \, du = \frac{1}{2} u^2 \quad \text{bir yerleştirme yapalım:} \quad u = \ln x \Rightarrow du = \frac{1}{x}dx
Bu yüzden:
\int u \, du = \frac{1}{2}(\ln x)^2 \quad \text{Şimdi sınırları uygulayalım:}
\int_{1}^{e} \frac{\ln x}{x} dx = \left[ \frac{1}{2} (\ln x)^2 \right]_{1}^{e}
Sınırları yerine koyarak:
\left[ \frac{1}{2} (\ln e)^2 \right] - \left[ \frac{1}{2} (\ln 1)^2 \right] = \frac{1}{2} (1)^2 - \frac{1}{2} (0)^2 = \frac{1}{2} (1) - \frac{1}{2} (0) = \frac{1}{2}
4. Hacimi hesaplayalım
V = 2\pi \times \frac{1}{2} = \pi
Sonuç olarak:
Sınırları (x = 1) ve (x = e) olan y-eksenine döndürülen bölgenin hacmi \boxed{\pi}'dir.