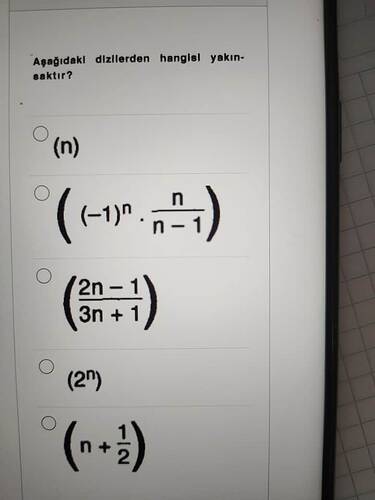
Aşağıdaki dizilerden hangisi yakınsaktır?
Cevap:
Bir dizinin yakınsak (convergent) olup olmadığını belirlemek için, dizinin limitinin var olup olmadığına ve bir sonlu değere mi yaklaştığına bakmamız gerekir. Bu diziler arasından yalnızca limitleri belirli olan diziler yakınsaktır. Bu nedenle, her seçeneği aşağıda inceleyelim:
-
(n) Dizisi
- \lim_{{n \to \infty}} n = \infty
- Bu dizi diverjandır; çünkü ( n ) sonsuzluğa gider.
-
\left( (-1)^n \cdot \frac{n}{{n-1}} \right) Dizisi
- ( \left( (-1)^n \cdot \frac{n}{n-1} \right) = \left( (-1)^n \cdot \left( 1 + \frac{1}{n-1} \right) \right) )
- Bu dizi osilasyon yapar ve sabit bir değere yakınsanmaz; dolayısıyla bu dizi de diverjandır.
-
\left( \frac{2n-1}{3n+1} \right) Dizisi
- \lim_{{n \to \infty}} \frac{2n-1}{3n+1} = \frac{2}{3}
- Bu dizi bir sonlu değere (2/3) yakınsar.
-
(2^n) Dizisi
- \lim_{{n \to \infty}} 2^n = \infty
- Bu dizi de diverjandır; çünkü ( n ) sonsuzluğa giderken ( 2^n ) da sonsuzluğa gider.
-
\left( n + \frac{1}{2} \right) Dizisi
- \lim_{{n \to \infty}} \left( n + \frac{1}{2} \right) = \infty
- Bu dizi de diverjandır; çünkü ( n ) sonsuzluğa giderken dizi de sonsuzluğa doğru yaklaşıyor.
Sonuç olarak, sadece 3. seçenek ( \frac{2n-1}{3n+1} ) dizisi \frac{2}{3} limitine sahip ve yakınsaktır.
Doğru cevap: \left( \frac{2n-1}{3n+1} \right)