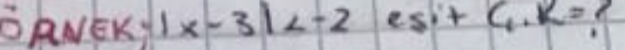 güçlü metin Ix-3I<-2 ÇÖZÜM KÜMESİ=?
güçlü metin Ix-3I<-2 ÇÖZÜM KÜMESİ=?
Resimde verilen eşitsizlik şu şekilde:
$$|x - 3| \leq 2$$
Bu tür eşitsizlikleri çözmek için mutlak değerden kurtulmamız gerekiyor. Mutlak değer eşitsizliği \leq ile verildiği için, aşağıdaki gibi iki olasılığı ele alıyoruz:
- x - 3 \leq 2
- x - 3 \geq -2
Şimdi bu eşitsizlikleri çözelim:
-
x - 3 \leq 2
- Her iki tarafa da 3 ekleyelim: x \leq 5
-
x - 3 \geq -2
- Her iki tarafa da 3 ekleyelim: x \geq 1
Bu iki sonucu birleştirirsek; çözüm kümesi 1 \leq x \leq 5 olur. Bu, x'in 1 ile 5 arasında (1 ve 5 dahil) değerler alabileceği anlamına gelir.
Bu eşitsizlik, belirli bir aralıkta çözüm kümesine sahip olduğundan boş küme değildir. Boş küme, belirli bir çözüm kümesi olmadığı anlamına gelir. Ancak bu örnekte x için bir çözüm aralığı bulduk.
Ix-3I<-2 ÇÖZÜM KÜMESİ=?
BUNU SORDUM
Anladım, özür dilerim.
Eşitsizlik: ( |x - 3| < -2 )
Mutlak değerli bir ifadenin negatif bir sayıdan küçük olması mümkün değildir. Çünkü mutlak değer daima pozitif ya da sıfırdır.
Bu yüzden, bu eşitsizliğin çözüm kümesi boş küme ( \emptyset ) olacaktır.