Doğrusal Hareket Problemi Çözümü
Problem:
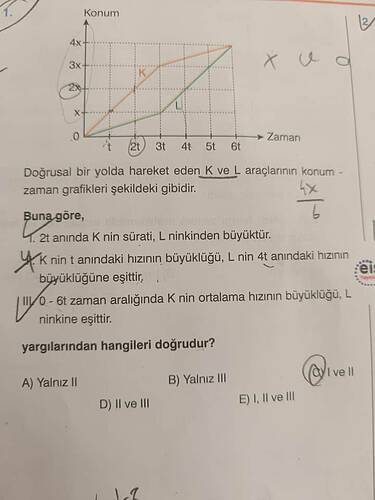
Doğrusal bir yolda hareket eden ( K ) ve ( L ) araçlarının konum-zaman grafikleri yukarıdaki gibidir. Buna göre aşağıdaki yargılardan hangileri doğrudur?
Yargılar:
- (2t) anında (K)nin sürati, (L)ninkinden büyüktür.
- (K)nin (t) anındaki hızının büyüklüğü, (L)nin (4t) anındaki hızının büyüklüğüne eşittir.
- (0 - 6t) zaman aralığında (K)nin ortalama hızının büyüklüğü, (L)ninkine eşittir.
Seçenekler:
A) Yalnız II
B) Yalnız III
C) I ve II
D) II ve III
E) I, II ve III
Çözüm:
-
Yargı I: (2t) anında ( K )nin sürati, ( L )ninkinden büyüktür mi?
-
Hız, konum-zaman grafiğinde eğim olarak gösterilir. ( K ) grafiğinde ( t ) ile ( 2t ) aralığında konum ( X )ten ( 4X )e kadar artarken zaman ( t )'den ( 2t )'ye artıyor. Bu yüzden ( K )'nin ( t - 2t ) aralığındaki hızı:
v_K = \frac{\Delta x}{\Delta t} = \frac{4X - X}{2t - t} = \frac{3X}{t} -
( L ) grafiğinde ise ( t ) ile ( 2t ) arasında konum ( 0 )'dan ( 2X )'e kadar artıyor. Bu yüzden ( L )'nin ( t - 2t ) aralığındaki hızı:
v_L = \frac{\Delta x}{\Delta t} = \frac{2X - 0}{2t - t} = \frac{2X}{t} -
Görülüyor ki ( v_K = \frac{3X}{t} ) ve ( v_L \frac{2X}{t} ), bu nedenle ( v_K > v_L ). Yani, birinci yargı doğru.
-
-
Yargı II: ( K )nin ( t ) anındaki hızının büyüklüğü, ( L )nin (4t ) anındaki hızının büyüklüğüne eşittir mi?
-
( t ) anında ( K )`nin hızı:
v_K(t) = \frac{X - 0}{t - 0} = \frac{X}{t} -
( 4t ) anında ( L )nin hızı:
v_L(4t) = \frac{6X - 2X}{6t - 2t} = \frac{4X}{4t} = \frac{X}{t} -
Bu hızlar birbirine eşittir. Yani ikinci yargı doğru.
-
-
Yargı III: (0 - 6t) zaman aralığında (K)nin ortalama hızının büyüklüğü, (L)ninkine eşittir mi?
-
Ortalama hız, toplam yer değiştirme bölü toplam zamandır.
-
( K )nin ( 0 - 6t ) aralığındaki yer değiştirmesi:
\Delta x_K = 2X - 0 = 6X -
Toplam zaman: ( 6t )
v_{ort,K} = \frac{6X}{6t} = \frac{X}{t} -
( L )`nin ( 0 - 6t ) aralığındaki yer değiştirmesi:
\Delta x_L = 6X - 0 = 6X -
Toplam zaman: ( 6t )
v_{ort,L} = \frac{6X}{6t} = \frac{X}{t} -
Bu hızlar birbirine eşittir. Yani üçüncü yargı da doğru.
-
Sonuç:
Bütün yargılar doğru olduğundan, doğru cevap “E) I, II ve III” olacaktır.