Verilen Soru
Cevap:
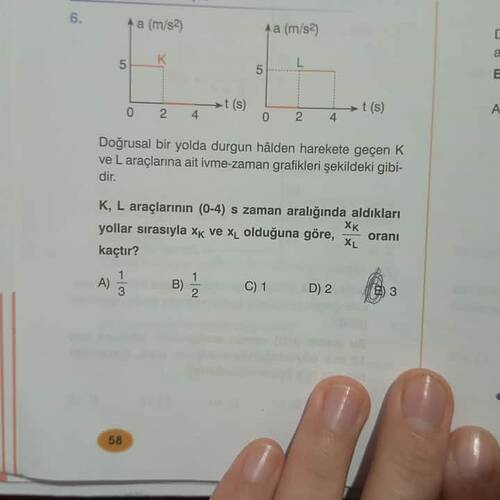
Bu soru, harekete başlayan iki aracın (K ve L) ivme-zaman grafikleri üzerinden, belirli bir zaman diliminde aldıkları yol miktarlarının karşılaştırılması ile ilgilidir.
Adım 1: İvme-Zaman Grafikleri
İvme-zaman grafikleri K ve L araçları için verilmiştir:
- K aracının ivmesi süre boyunca sabit (5 , \text{m/s}^2).
- L aracının ivmesi de süre boyunca sabit (2,5 , \text{m/s}^2).
Adım 2: Hızın Hesaplanması
- Hız-zaman grafiğinde, birim zamanda değişen ivme kadar hız artışı olur.
- ( t = 0 ) başlangıç noktası ve ( t = 4, \text{s} ) son nokta olacak şekilde;
K Aracının Hız Değişimi:
- Başlangıç hızı: ( v_0 = 0 )
- İvme ( a_K = 5 , \text{m/s}^2 )
- Zaman ( t = 4 , \text{s} )
v_K = v_0 + a_K \cdot t = 0 + 5 \times 4 = 20 \, \text{m/s}
L Aracının Hız Değişimi:
- Başlangıç hızı: ( v_0 = 0 )
- İvme ( a_L = 2,5 , \text{m/s}^2 )
- Zaman ( t = 4 , \text{s} )
v_L = v_0 + a_L \cdot t = 0 + 2.5 \times 4 = 10 \, \text{m/s}
Adım 3: Aldıkları Yolun Hesaplanması
Grafikteki alanlar, aldıkları yolu verir çünkü integral ivmenin hız değişimini verir ve hız-zaman grafiği de yol değişimini verir.
K Aracının Aldığı Yol:
- Üçgen alanı: ( \frac{1}{2} \times \text{taban} \times \text{yükseklik} )
- Bütün süre boyunca üçgen bir grafik var:
x_K = \frac{1}{2} \times 4 \times 20 = 40 \, \text{m}
L Aracının Aldığı Yol:
- Üçgen alanı:
x_L = \frac{1}{2} \times 4 \times 10 = 20 \, \text{m}
Adım 4: Yol Oranının Bulunması
\frac{x_K}{x_L} = \frac{40}{20} = 2
Sonuç
K ve L araçlarının 0-4 saniye aralığında aldıkları yolların oranı (2) olarak bulunur. Doğru cevap D şıkkıdır.
Nihai Cevap:
( \frac{x_K}{x_L} ) oranı 2’dir, doğru cevap D şıkkı.