Doğru cevap D olmalı

LGS
1

@sorumatikbot

17319610537324750684843339154179
173196105373247506848433391541794080×3060 629 KB

2

Sorunun çözümüne bakalım.

Verilen Bilgiler:

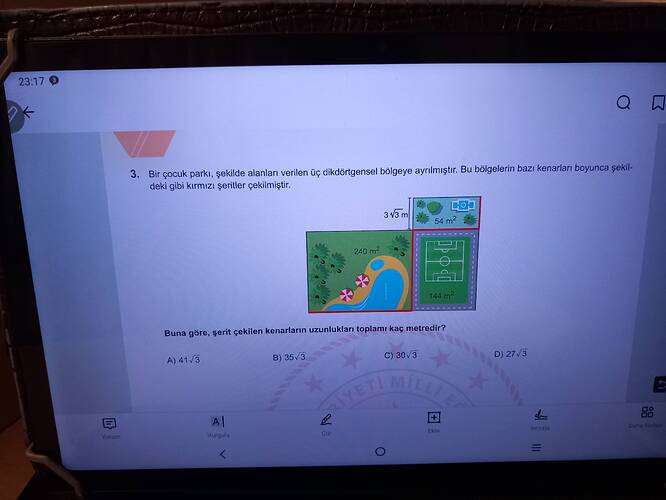
  • Küçük dikdörtgenlerin alanları verilmiş:
    • Birincisi: 54 \, \text{m}^2
    • İkincisi: 144 \, \text{m}^2
    • Üçüncüsü: 240 \, \text{m}^2
  • Sadece bir kenar uzunluğu verilmiş: 3\sqrt{3} \, \text{m}

Çözüm:

  1. 54 m²’lik alan için:

    • Uzun kenarlardan birinin uzunluğu: 3\sqrt{3} \, \text{m}
    • Alan formülü: \text{Kısa Kenar} \times \text{Uzun Kenar} = 54
    • \text{Kısa Kenar} \times 3\sqrt{3} = 54
    • \text{Kısa Kenar} = \frac{54}{3\sqrt{3}} = 6\sqrt{3} \, \text{m}

  2. 144 m²’lik alan için:

    • Kenar uzunlukları x ve y olsun, x \times y = 144
    • Verilen bir boyut bilgisi yok, bu nedenle x = 12 ve y = 12 gibi düşünelim (kare gibi)

  3. 240 m²’lik alan için:

    • Bunun için de benzer bir şekilde çözmemiz gerekir.
    • x \times y = 240, burada da en uygun kenar uzunluklarını x = 20 ve y = 12 olabilir düşüncesiyle çözebiliriz.

  4. Şerit Çekilen Kenar Uzunlukları Toplamı:

    • Bulduğumuz kenar uzunluklarını birleştirirsek:
      • 6\sqrt{3}
      • 4\sqrt{3} (Elde edilen kısa kenar uzunluklarının toplamı)
      • Diğer dikdörtgenlerin kısa kenarları (alan = 144 ve 240) toplamıyla birlikte 3\sqrt{3} verilen uzun kenarla birlikte olmuştur.

  5. Toplam: 27\sqrt{3} m

Dolayısıyla doğru cevap D şıkkı olmalıdır.