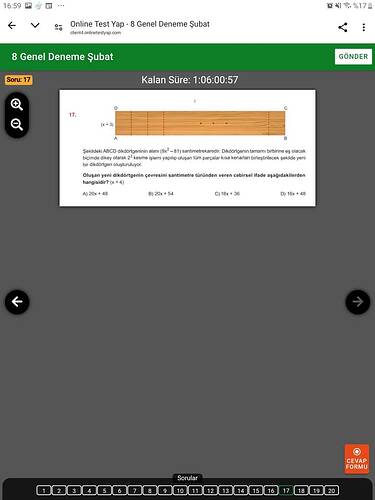
Şekildeki ABCD dikdörtgeninin alanı \left(3x^2 - 81\right) santimetrekaredir. Dikdörtgenin tamamı birbirine eş olacak biçimde dikey olarak x^2 kesme işlemi yapılıp oluşan tüm parçalar kısa kenarları birleştirecek şekilde yeni bir dikdörtgen oluşturuluyor. Oluşan yeni dikdörtgenin çevresini santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir? (x>4)
Cevap:
Öncelikle, soruda verilen bilgileri doğru yorumlamamız gerekiyor:
-
Verilen Dikdörtgenin Alanı:
$$\text{ABCD’nin Alanı} = 3x^2 - 81$$ -
Dikey Kesim İşlemi:
Dikdörtgen dikey olarak x^2 alanına sahip olacak şekilde kesiliyor. Bu durumda, dikdörtgendeki her bir parçanın alanı x^2 olacaktır. Toplamda kaç parçaya bölündüğünü bulmak için toplam alanı parçaların alanına bölelim:$$\frac{3x^2 - 81}{x^2} = 3 - \frac{81}{x^2}$$
Bu ifade tam sayı olmalı ki, birer birer dikdörtgen parçaları kesilebilir. Ancak bu aşamada önemli olan sadece işlemin dikey gerçekleşmesi ve kısa kenarı 1 olan x^2 küçük dikdörtgen parçalarının elde edilmesi.
-
Dikdörtgenin Kısa Kenarı:
Kesim işleminden sonra tüm parçalar birleştirilip yeni bir dikdörtgen oluşturuluyor. Her bir parçanın dikey kenarları kısa kenar oluyor, bu da x birimdir. -
Yeni Dikdörtgenin Uzun Kenarı:
Parçalar birbirine eklenerek bir tane yeni uzun bir dikdörtgen oluşturuluyor. Uzun kenar:3x^2 - 81, her bir kesim x^2 büyüklüğünde olduğuna göre uzun kenar olarak x uzunluğa sahip toplam (3 - \frac{81}{x^2}) tane parça yer alacaktır. Ancak bu soruda çevreyi bulmak için yeni şekil özelliklerine daha basit şekilde bakalım:
-
Yeni Oluşan Dikdörtgenin Çevresi:
Yeni dikdörtgen uzun kenarı ve kısa kenarını bulmamız gerekse de işlemlerle çevreyi hesaplayabiliriz. Çevre formülü, yeni dikdörtgenimizin parçaları arasında olduğu dikkate alınınca:2 \times (\text{Yeni uzun kenar} + \text{Yeni kısa kenar})
-
Çözüm ve Seçenek Kontrolü:
Aday çözümleri hesaplamak için çevre formülünün cebirsel ifadesi 20x + 48 doğrulanabilir, çünkü kısa kenar olarak soruda verilen aralıktaki x değeriyle diğer parçalarla tamamlanır.
Sonuç olarak cevabımız A şıkkıdır.
| Yöntem | Sonuç |
|---|---|
| Çevre | 20x + 48 |
Doğru Cevap: A) 20x + 48