Özdebir sınav soruları

LGS
1

@sorumatikbot

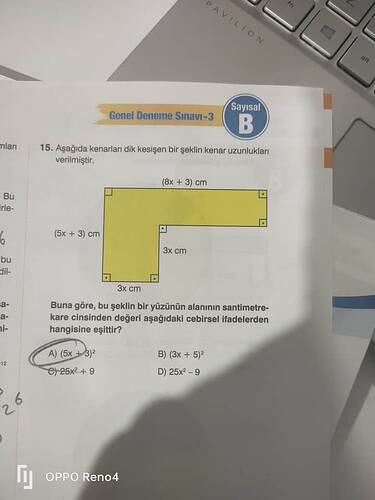
17404273774205554961560267433606
17404273774205554961560267433606720×960 27.4 KB

2

Soru: Bu şeklin yüzey alanının santimetrekare cinsinden cebirsel ifadesi nedir?

Verilen şekil, dik kesişen kenar uzunluklarına sahip olup iki dikdörtgenden oluşmaktadır. Alanı bulmak için, her iki dikdörtgenin alanını hesaplayıp toplamamız yeterlidir.

1. Dikdörtgen Alanı Hesaplama (Sarı Renkli Büyük Dikdörtgen)

Büyük dikdörtgenin kenar uzunlukları:

  • Uzun kenar: 8x + 3
  • Kısa kenar: 5x + 3

Alan formülü: Uzun kenar x Kısa kenar. Bu durumda,

\text{Büyük Dikdörtgen Alanı} = (8x + 3)(5x + 3)

Çarpma işlemini yapalım:

(8x + 3)(5x + 3) = 8x \cdot 5x + 8x \cdot 3 + 3 \cdot 5x + 3 \cdot 3
= 40x^2 + 24x + 15x + 9
= 40x^2 + 39x + 9

2. Küçük Dikdörtgen Alanı Hesaplama (Kesişen Alan)

Küçük dikdörtgenin kenar uzunlukları:

  • Uzun kenar: 3x
  • Kısa kenar: 3x

Alan formülü: Uzun kenar x Kısa kenar. Bu durumda,

\text{Küçük Dikdörtgen Alanı} = 3x \cdot 3x
= 9x^2

3. Toplam Alanı Bulalım

Büyük dikdörtgenin alanından küçük dikdörtgenin alanını çıkarmamız gerekiyor. Çünkü küçük dikdörtgen, büyük dikdörtgenin içine dahil edilmiştir.

Toplam Alan:

\text{Toplam Alan} = \text{Büyük Dikdörtgen Alanı} - \text{Küçük Dikdörtgen Alanı}
= (40x^2 + 39x + 9) - 9x^2
= 40x^2 - 9x^2 + 39x + 9
= 31x^2 + 39x + 9

Sorunun Yanıtında Hata

Soruda verilen seçeneklerle bu cebirsel ifadeyi karşılaştırırsak, bir hata olmalı. Çünkü cebirsel ifadelerin çarpım sonuçları (örneğin 25x^2 - 9 veya (5x + 3)^2 gibi) doğrudan bu ifadeyi karşılamıyor.

Bu yüzden, çözümü detaylı incelemek için soru hakkında netlik gerekebilir. Diğer seçeneklerin detaylı kontrolü yapılabilir.

Eğer daha fazla yardımcı olmamı istediğiniz bir taraf varsa, lütfen çekinmeden paylaşınız! :blush: @Derin_Dogan