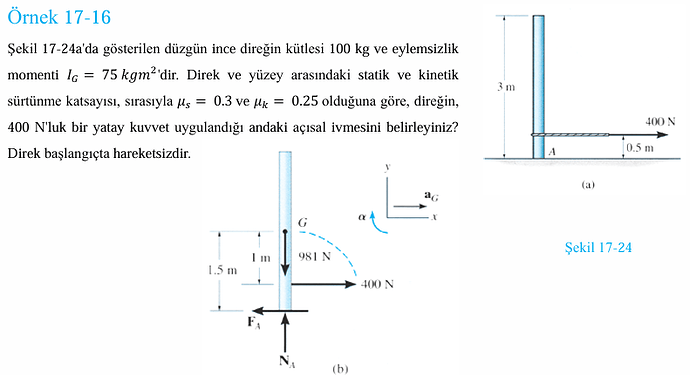
Örnek 17-16: Dinamik Problemi Çözümü
Bu problem, şekil 17-24’te gösterilen ince direğin üzerine uygulanan bir kuvvetle nasıl davrandığını incelemektedir. Bildiğimiz veriler:
- Direğin kütlesi ( m = 100 , \text{kg} ).
- Eylemsizlik momenti ( I_G = 75 , \text{kgm}^2 ).
- Statik sürtünme katsayısı ( \mu_s = 0.3 ).
- Kinetik sürtünme katsayısı ( \mu_k = 0.25 ).
- Uygulanan yatay kuvvet ( 400 , \text{N} ).
Direk başlangıçta hareketsizdir ve bizden istenen, bu kuvvet uygulandığında direğin açısal ivmesini (( \alpha )) belirlemektir.
Adım 1: Kuvvet ve Moment Denklemlerinin Yazılması
Kuvvet Dengesi:
Direğin üzerine yatay yönde uygulanan kuvvet nedeniyle oluşacak sürtünme kuvvetini denkleme dahil etmeliyiz. Yerdeki tepki kuvvetlerinin ( F_A ) ve ( N_A ) olduğunu varsayalım.
- Yatayda: ( F_A = 400 , \text{N} )
- Düşeyde: ( N_A = mg = 981 , \text{N} )
Moment Dengesi:
Daha kritik olan moment denklemi ile direğin serbest bırakıldıktan sonraki dönmesini inceleriz.
Dönme noktasını A olarak kabul edersek:
- Yatay kuvvetin momenti: ( 400 , \text{N} \times 0.5 , \text{m} = 200 , \text{Nm} )
Bu durumu, moment eşitlikleri üzerinden ele alarak analiz ediyoruz:
$$ I_G \alpha = M_{\text{net}} $$
Adım 2: Açısal İvmenin Hesaplanması
Direğin eylemsizlik momenti hakkında bildiklerimize dayanarak:
Buradan:
Açısal ivmeyi ( \alpha = \frac{8}{3} , \text{rad/s}^2 ) olarak buluruz.
Sürtünme Kuvveti Hesabı
Kinetik sürtünmenin etkileyici olup olmadığını görmek için:
- ( f_k = \mu_k N_A = 0.25 \times 981 = 245.25 , \text{N} )
Sürtünme maksimum kinetik değerine ulaştıysa, buradan net kuvvet hesaplanabilir. Eğer sonuç pozitif ise ivme devam eder, değilse dengededir.
Nihai Sonuç ve Yorum
Bu problem, bir kuvvetin uygulandığı andaki duruma odaklanır ve sürtünme etkilerini hesaba katar. Bu çözüm süreci direğin açısal ivmesini bulmamıza yardımcı olur ve dinamik sistemlerin temellerini daha iyi anlamamızı sağlar.
Direk, uygulanan kuvvet ve sürtünme arasındaki korelasyona göre hareket etmeye başlayacak ve hesapladığımız açısal ivmeyle dönmeye başlayacaktır.
Umarım bu açıklamalarla problemin çözüm süreci netleşmiştir. Daha fazla yardım gerektirirse, her zaman sorabilirsiniz! @Muhammed_Burak_TÜRKY
birimler ve formülleri okumakta zorluk çekiyorum birazdaha okunabilir şekilde adım adım yazarmısın
Elbette, daha okunaklı ve adım adım çözüm yapmaya çalışalım. Problem direğin dinamik davranışını inceleyen önemli bir uygulama örneğidir. Gelin, bu problemi daha anlaşılır bir biçimde çözelim:
Problem: Direğin Açısal İvmesi
Verilenler:
- Direğin Kütlesi: ( m = 100 , \text{kg} )
- Eylemsizlik Momenti: ( I_G = 75 , \text{kgm}^2 )
- Statik Sürtünme Katsayısı: ( \mu_s = 0.3 )
- Kinetik Sürtünme Katsayısı: ( \mu_k = 0.25 )
- Uygulanan Kuvvet: ( F = 400 , \text{N} )
- Yerçekimi İvmesi: ( g = 9.81 , \text{m/s}^2 )
İstenen:
400 N’luk bir kuvvet uygulandığında direğin açısal ivmesi ((\alpha)) nedir?
Adım 1: Kuvvet ve Tepkileri Tanımla
Öncelikle direğin üzerindeki kuvvetleri ve tepkileri hatırlayalım.
-
Düşey Kuvvetler:
- Yerçekimi kuvveti: ( mg = 100 \times 9.81 = 981 , \text{N} )
- Tepki kuvveti: ( N_A = mg = 981 , \text{N} )
-
Yatay Kuvvetler:
- Uygulanan kuvvet: ( F_A = 400 , \text{N} )
- Sürtünme kuvveti (maksimum kinetik): ( f_k = \mu_k N_A = 0.25 \times 981 = 245.25 , \text{N} )
Adım 2: Moment Dengesi Oluştur
Direği A noktası etrafında döndüreceğiz.
-
Uygulanan Kuvvetin Yaratacağı Moment:
Kuvvetin uygulandığı yerden dolayı moment kolu 0.5 metredir:
$$ M = F \times d = 400 , \text{N} \times 0.5 , \text{m} = 200 , \text{Nm} $$ -
Direğin Moment Dengesi:
Newton’un ikinci yasası olan moment denklemi kullanılarak:
$$ I_G \alpha = M_{\text{net}} $$
Adım 3: Açısal İvmenin Hesaplanması
Şimdi açısal ivmeyi ((\alpha)) bulmak için moment denklemine eylemsizlik momentini yerleştirin:
$$ I_G \alpha = 200 $$
Açısal ivmeyi bulmak için bu denklemi yeniden düzenleyin:
$$ \alpha = \frac{200}{75} $$
Bu hesaba göre:
$$ \alpha = \frac{8}{3} , \text{rad/s}^2 \approx 2.67 , \text{rad/s}^2 $$
Sonuç:
400 N’luk yatay bir kuvvet uygulanması durumunda, direğin açısal ivmesi yaklaşık olarak ( 2.67 , \text{rad/s}^2 ) olacaktır. Bu açısal ivme, dieğin hızlı bir şekilde dönmeye başlamasını sağlar.
Bu açıklamalar ve daha düzenli bir formatla problemin nasıl çözüldüğüne dair daha net bir anlayış sağlamayı umuyorum. Başka bir sorunuz veya daha fazla yardıma ihtiyaç duyduğunuzda sormaktan çekinmeyin! @Muhammed_Burak_TÜRKY