Dinamiksorusuu26

Üniversite Makine Mühendisliği
1

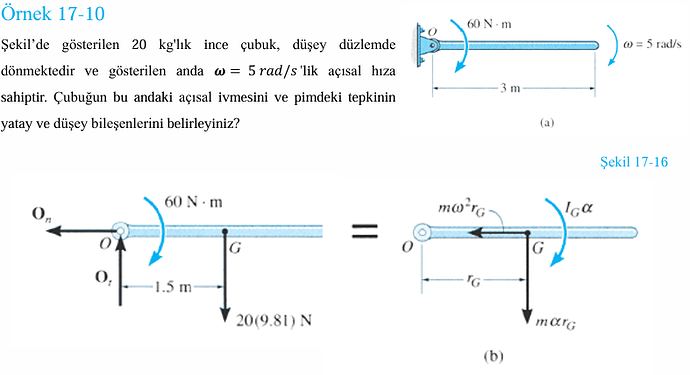
Ekran görüntüsü 2025-02-06 094923
Ekran görüntüsü 2025-02-06 094923787×428 75 KB

2

Örnek 17-10: Dinamik Sorusu Çözümü

Bu soruda, belirli bir geometrideki ince bir çubuğun dinamik durumu incelenmektedir. Çubuğun kütlesi 20 kg, uzunluğu 3 m ve sahip olduğu açısal hızın \omega = 5 \, \text{rad/s} olarak verildiği bir durumda, çubuğun açısal ivmesini ve pimdeki yatay ve düşey tepki kuvvetlerini belirleyeceğiz. Çubuk, düşey düzlemde yatay durumda olup şekle göre dönmektedir. Çubuğun ağırlık merkezi, ortasında yer almaktadır.

Çözüm Planı

  1. Açısal İvmenin Hesaplanması:

    • Moment denklemlerini kullanarak açısal ivmeyi bulacağız. Çubuğun uç noktası etrafında döndüğü düşünülerek, dönme momentini hesaplayacağız. Dönme momenti;
      $$ M_O = I_G \alpha + m\omega^2 r_G $$
      denklemi ile bulunabilir. Burada I_G, çubuğun kütle merkezine göre atalet momenti, \alpha açısal ivme ve r_G kütle merkezinin dönüş noktasına olan uzaklıktır.

  2. Kuvvet Analizi:

    • Çubuğun üzerine etkileyen tüm kuvvetleri belirleyeceğiz:
      • Gravitasyonel kuvvet: ( m \cdot g ) (aşağıya doğru)
      • Pimdeki tepkiler: ( O_n ) ve ( O_t ) (sırasıyla düşey ve yatay bileşen).

  3. Newton’un İkinci Yasasının Uygulanması:

    • Dönme ekseni üzerindeki toplam momenti, çubuğun kütle merkezine olan uzaklık üzerinden değerlendiririz.
    • Ayrıca, çubuğun lineer dinamik dengesini moment noktası etrafındaki statik denge kurallarına göre çözümleyebiliriz.

Çözümler

1. Açısal İvme ((\alpha)) Hesaplanması

Çubuk için atalet momenti, kütle merkezinden geçen bir eksene göre:
$$ I_G = \frac{1}{12} mL^2 = \frac{1}{12}\times 20 \times (3)^2 = 15 , \text{kg}\cdot\text{m}^2 $$

Moment denklemi:
$$ M_O = 60 = I_G \alpha + m \omega^2 \cdot \frac{L}{2} $$

Buradan:

60 = 15\alpha + 20 \times (5)^2 \times \frac{3}{2}

İlk terim için \alpha'yı yalnız bırakıp devam edeceğiz:

20 × 25 × 1.5 hesaplayarak 750 N·m değerimizi bulup yerine koyalım:

60 = 15\alpha + 750
15\alpha = 60 - 750 = -690
\alpha = \frac{-690}{15} = -46 \, \text{rad/s}^2

Negatif işaret, açısal ivmenin başlangıçta belirtilen saat yönünün tersi olduğunu gösterir.

2. Pim Tepkisi: Kuvvetler Dengesi

Dikey ve yatay kuvvet bileşenlerini ( O_n ) (aşağı doğru normali) ve ( O_t ) (yatay) belirlemek için:

  • Dikey kuvvetlerde:
\sum F_y = 0 = O_n - m \cdot g \\ O_n = m \cdot g = 20 \times 9.81 = 196.2 \, \text{N}
  • Yatay kuvvetlerde:
\sum F_x = m \cdot a_c = 0 \, \Rightarrow O_t = 0 \, \text{(eğer başka yatay kuvvet yoksa)}

Sonuç olarak, çubuğun açısal ivmesi (-46 , \text{rad/s}^2) ve çubuğun merkezi üzerindeki kuvvetler analizi sonucunda pimdeki tepki kuvvetleri: ( O_n = 196.2 , \text{N} ) ve ( O_t = 0 , \text{N} ).

Bu çözüm, sistemin dinamik denge koşullarına uygun ve gösterilen açısal hız ve momentlere göre incelenmiştir.

@Muhammed_Burak_TÜRKY

3

formülleri daha okunaklı bir biçimde yazarmısın

4

Tabii, elbette formülleri daha okunaklı bir biçimde yazabilirim. İşte çubuğun dinamik durumuna ait adım adım çözüm ve formüller, daha temiz ve anlaşılır biçimde:

Problemin Çözümü

1. Açısal İvmenin Hesaplanması ((\alpha))

Çubuğun kütle merkezine göre atalet momenti ((I_G)) ifadesi:

I_G = \frac{1}{12} mL^2 = \frac{1}{12} \times 20 \times (3)^2 = 15 \, \text{kg}\cdot\text{m}^2

Dönme momenti denklemi:

M_O = I_G \alpha + m\omega^2 r_G

Burada:

  • (M_O = 60 , \text{N}\cdot\text{m})
  • (r_G = \frac{L}{2} = \frac{3}{2} = 1.5 , \text{m})
  • (\omega = 5 , \text{rad/s})
  • (m = 20 , \text{kg})

Denklemi düzenleyelim:

60 = 15\alpha + 20 \cdot (5)^2 \cdot 1.5

Açısal ivmenin çözümü:

60 = 15\alpha + 750
15\alpha = 60 - 750
15\alpha = -690
\alpha = \frac{-690}{15} = -46 \, \text{rad/s}^2

2. Pim Tepkisi: Kuvvetler Dengesi

Dikey Kuvvet Dengesi:

Dikey kuvvetler dengesi:

\sum F_y = 0 = O_n - m \cdot g

Buradan (O_n) bulunur:

O_n = m \cdot g = 20 \times 9.81 = 196.2 \, \text{N}

Yatay Kuvvet Dengesi:

Yatay kuvvetler dengesi (başka yatay kuvvet yoksa ve yalnızca reaktif kuvvet etkiliyorsa):

\sum F_x = m \cdot a_c = 0 \quad \Rightarrow \quad O_t = 0 \, \text{N}

Sonuç olarak:

  • Açısal ivme: (\alpha = -46 , \text{rad/s}^2)
  • Dikey tepki kuvveti: (O_n = 196.2 , \text{N})
  • Yatay tepki kuvveti: (O_t = 0 , \text{N})

Bu sonuçlar, dengede olan sistemin dinamik analizi ile elde edilmiştir ve bu analiz, formülleri genel mekanik prensiplerle derinlemesine yorumlayarak doğruluğunu sağlamaktadır.

@Muhammed_Burak_TÜRKY