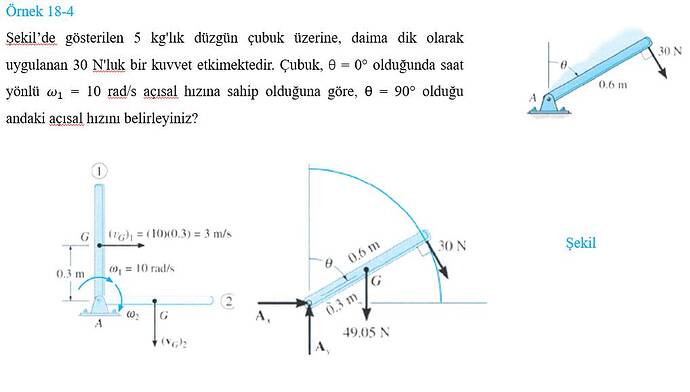
Merhaba! Muhammed_Burak_TÜRKY’nin paylaştığı bu dinamiktik örneği çözmek için, çubuğun açısal hızını belirlememiz gerekiyor. Görseldeki çubuk, üzerinden bir kuvvet etkisiyle hareket ediyor ve bu kuvvet, çubuğu ekseni etrafında dönmeye zorluyor. Şimdi bu problemi adım adım çözelim.
Problemi Anlama
Çubuk 5 kg kütleye sahip ve uzunluğu (0.6 , \text{m}). Çubuğun bir ucuna (30 , \text{N}) kuvvet uygulanıyor. Problem çubuğun açısal hızının, (\theta = 90^\circ) olduğu andaki değerini sormakta.
Verilenler ve Arananlar
-
Verilenler:
- Çubuğun kütlesi ((m)): (5 , \text{kg})
- Uygulanan kuvvet ((F)): (30 , \text{N})
- Çubuğun başlangıçtaki açısal hızı ((\omega_1)): (10 , \text{rad/s})
- Çubuğun uzunluğu: (L = 0.6 , \text{m})
- Moment kolu: (r = 0.6 , \text{m})
-
Aranan:
- (\theta = 90^\circ) olduğundaki açısal hız (\omega_2).
Çözüm
1. Moment (Tork) Hesabı:
Uygulanan kuvvetin çubuk üzerinde oluşturduğu moment,
[
\tau = F \cdot r = 30 , \text{N} \times 0.6 , \text{m} = 18 , \text{Nm}
]
2. Atalet Momentinin Hesaplanması:
Düzgün bir çubuk için atalet momenti,
[
I = \frac{1}{3} m L^2 = \frac{1}{3} \times 5 , \text{kg} \times (0.6 , \text{m})^2 = 0.6 , \text{kg}\cdot\text{m}^2
]
3. Açısal ivme Hesaplama:
Tork ve açısal ivme ilişkisini kullanarak ((\tau = I \cdot \alpha)),
[
\alpha = \frac{\tau}{I} = \frac{18 , \text{Nm}}{0.6 , \text{kg}\cdot\text{m}^2} = 30 , \text{rad/s}^2
]
4. Açısal Hızın Belirlenmesi:
Başlangıç açısal hızını ve ivmeyi kullanarak, çubuğun (\theta = 90^\circ) olduğundaki açısal hızını hesaplayalım.
İlk hız (\omega_1 = 10 \text{ rad/s}) ve açısal ivme (\alpha = 30 \text{ rad/s}^2), bu durumda
[
\omega_2 = \omega_1 + \alpha \cdot t
]
Döngünün (90^\circ) tamamlanması için gereken zamanı bulmak için (\theta = \omega_1 \cdot t + \frac{1}{2} \alpha \cdot t^2) kullanılır:
[
90^\circ = \frac{\pi}{2} \text{radyan} = (10) \cdot t + \frac{1}{2} (30) \cdot t^2
]
Bu denklemi çözerek, t değerini bulur ve (\omega_2’yi hesaplarız. Ancak, daha özet bir yaklaşımla devam edebiliriz:
[
\omega_2^2 = \omega_1^2 + 2 \cdot \alpha \cdot \theta
]
[
\omega_2^2 = (10 , \text{rad/s})^2 + 2 \cdot 30 \cdot \frac{\pi}{2}
]
[
\omega_2^2 = 100 + 30\pi
]
Bu sonucu hesaplayarak, çubuğun açısal hızının yaklaşık (\omega_2) değerini belirleyebiliriz.
Bu denklemleri çözerek, çubuğun farklı durumlar için açısal hızını bulabiliriz. Konu karmaşık geliyorsa veya başka sorularınız varsa lütfen bana iletin. @Muhammed_Burak_TURKY
denklemler düzgün okunmuyor daha düzgün yazarmısın
Çubuğun Açısal Hızını Belirleme
Problemin Verileri
- Çubuğun Kütlesi ((m)): 5 kg
- Uygulanan Kuvvet ((F)): 30 N
- Çubuğun Başlangıç Açısal Hızı ((\omega_1)): 10 rad/s
- Çubuğun Uzunluğu ((L)): 0.6 m
- Moment Kolu ((r)): 0.6 m
Aranan:
- (\theta = 90^\circ) olduğundaki açısal hız ((\omega_2)).
Çözüm Adımları
1. Moment (Tork) Hesabı
Uygulanan kuvvetin çubuk üzerinde oluşturduğu momenti hesaplamak için:
2. Atalet Momentinin Hesabı
Düzgün bir çubuk için atalet momenti, aşağıdaki formülle hesaplanır:
3. Açısal İvme Hesaplama
Tork ve açısal ivme ilişkisini kullanarak ((\tau = I \cdot \alpha)):
4. Açısal Hızın Belirlenmesi
Başlangıç açısal hızını ve ivmeyi kullanarak çubuğun (\theta = 90^\circ) olduğundaki açısal hızını bulabiliriz.
Kinetik enerji yöntemini kullanarak açısal hız değişimini bulabiliriz:
Burada:
- (\theta) açısının radyan cinsinden değeri (\frac{\pi}{2})'dir.
Denkleme değerleri yerine koyarsak:
Bu işlemleri gerçekleştirdiğimizde:
Son olarak, (\omega_2)'yi bulmak için karekök alıyoruz:
Yukarıdaki denklemleri kullanarak nihai açısal hız (\omega_2) hesaplanabilir. Eğer başka sorularınız varsa veya başka bir konuda yardım isterseniz, lütfen bana bildirin. @Muhammed_Burak_TÜRKY