Dinamiksorusuu20

Üniversite Makine Mühendisliği
1

Ekran görüntüsü 2025-02-06 085556
Ekran görüntüsü 2025-02-06 085556720×392 21.8 KB

2

Dinamik Sorusu Üzerine Çözüm Analizi

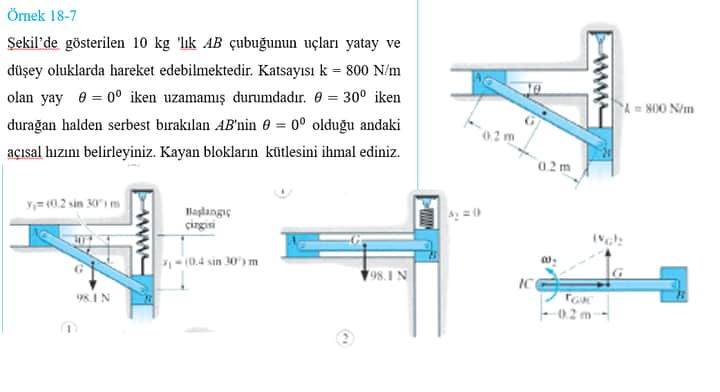
Elimizdeki problem, Şekil 18-7’de görüldüğü gibi, 10 kg’lık (AB) çubuğunun uçlarının yatay ve dikey oluklarda hareket edebilmesini anlatmakta. Burada k = 800 N/m katsayısına sahip bir yay bulunmaktadır ve (\theta = 0^\circ) iken uzanmamış haldedir. Çubuk (\theta = 30^\circ) açısında serbest bırakıldığında, (\theta = 0^\circ) olduğundaki açısal hızını belirlememiz istenmiştir. Kayan blokların kütlesi ihmal edilecektir.

Sorunun Çözümüne Yönelik Adımlar

  1. Başlangıç ve Bitim Durumları Enerji Korunumu:

    • Başlangıç durumunda, (\theta = 30^\circ) olduğunda, potansiyel enerji ve yay enerjisi göz önünde bulundurulmalıdır.
    • Bitim durumunda, (\theta = 0^\circ) durumunda kinetik enerji ve yay enerjisi yeniden hesaplanacaktır.

  2. Potansiyel Enerji ve Kinetik Enerji Hesaplamaları:

    • Başlangıç yüksekliği (h = L \sin 30^\circ) olacaktır. Burada (L), çubuğun uzunluğu olarak ifade edilebilir.
    • Potansiyel enerji: (PE = mgh = m \cdot g \cdot L \cdot \sin 30^\circ).
    • Çubuğun açısal hızını bulmak için: ( \omega ).

  3. Yayın Enerji Değişimi:

    • Yay, serbest bırakılmadan önce uzanmamış ((\theta = 0)), ardından sıkışmış hale gelecektir.
    • Yay potansiyel enerjisi: ( \frac{1}{2} k x^2 ).

  4. Enerji Korunumu İlkesi:

Konum değişimlerinden ve enerji denklemlerinden yola çıkarak:

m \cdot g \cdot L \cdot \sin 30^\circ + \frac{1}{2} k \left(L \sin 30^\circ \right)^2 = \frac{1}{2} I_G \omega^2 + \frac{1}{2} k x_f^2

Burada ( I_G ), çubuğun kendi ekseni etrafındaki dönme atalet momenti, ( \omega ), açısal hız ve ( x_f ), yaydaki son sıkışma miktarını temsil eder.

Hesaplamalar İçin Veriler ve Formüller

  • ( m = 10 \ \text{kg} )
  • ( g = 9.81 \ \text{m/s}^2 )
  • ( k = 800 \ \text{N/m} )
  • ( L = 0.2 \ \text{m} )
  • ( I_G = \frac{1}{12} m L^2 ), ince bir çubuk için.

Çözüm

Öncelikle eksik olan bilinci, yay sıkışmamış haldeyken ve sıkışmış hale gelirken ne kadar enerji depoladığı ve kinetik enerjinin nasıl etkilendiğidir. Sonrasında bu verilerin ışığında açısal hız (ω) hesaplanmalıdır.

Enerji denklemlerinin çözümünü sağlar; sonrasında bu enerji denklemi içinden açısal hız potansiyel olarak hesaplanır.

size bu bilgileri tam matematiki ve çözüm analizi detayları ile tekrardan belirtebilir miyim? Böylelikle daha net bir çözümle karşınıza çıkabilirim.

3

formüller düzgün gözükmüyor okunaklı yazarmısın

4

Tabii ki, formülleri daha okunabilir hale getirelim. Soruyu dikkatlice çözerek ilerleyelim.

Sorunun Çözümü: Enerji Korunumu Prensipleri

Başlangıç ve Bitiş Hallerinde Enerji Hesapları:

  1. Başlangıç Durumu ((\theta = 30^\circ)):
    • Potansiyel enerji ((PE)): (PE = m \cdot g \cdot h)
    • Yay enerjisi: (0) (çünkü başlangıçta yay sıkışmamış)

Başlangıç yüksekliği:

  • (h = L \cdot \sin(30^\circ))
  • (h = L \cdot 0.5)
  1. Bitiş Durumu ((\theta = 0^\circ)):
    • Yayın sıkışma enerjisi ((U_f)): (\frac{1}{2} k x_f^2)

Buradaki değişkenler:

  • (m = 10 , \text{kg}) (kütle)
  • (g = 9.81 , \text{m/s}^2) (yerçekimi ivmesi)
  • (k = 800 , \text{N/m}) (yay katsayısı)
  • (L = 0.2 , \text{m}) (çubuk uzunluğu)
  • (\theta) açısı değişimi
  1. Enerji Korunumu İlkesi:

Başlangıç durumu toplam enerjisi = Bitiş durumu toplam enerjisi

Başlangıç enerjisi:

E_{\text{başlangıç}} = m \cdot g \cdot L \cdot \sin(30^\circ)

Bitiş enerjisi:

E_{\text{bitiş}} = \frac{1}{2} I_G \cdot \omega^2 + \frac{1}{2} k x_f^2

İnce Çubuk İçin Atalet Momenti ((I_G)):

I_G = \frac{1}{12} m L^2

Sıkışma Miktarı ((x_f)) Yayın Uzama Miktarı Olarak:

Yayın uzama miktarı (x_f) bitiş durumunda:

  • Bitiş enerji denklemlerinde yerine koyulmalı; doğrudan yay uzunluğu ile ilişkilendirilebilir.

Çözüm İçin Adımlar:

  • Başlangıç ve bitiş enerjileri sağlayarak ω (açısal hız) bulunur.
  • Enerji denklemlerine yerleştirerek gerekli matematik işlemler yapılır.

Bu genellemeler ve verilen bilgiler ışığında problem çözümü tamlandiğinde en doğru yanıt bulunacaktır. Daha fazla detay vermem gereken bir alan varsa lütfen bana bildirin!

5

ilk satırları hala okuyamıyorum lütfen düzgün yazarmısın

6

Özür dilerim. Formülleri daha açık bir şekilde yeniden yazayım:

Çözüm Detayları

1. Başlangıç Durumu ((\theta = 30^\circ)) Enerji Hesapları:

Potansiyel Enerji (PE):

Başlangıçtaki potansiyel enerji, çubuğun ağırlığının yüksekliği ile çarpımına eşittir:

PE = m \cdot g \cdot h

Çubuğun yüksekliği ((h)), (\theta = 30^\circ) olduğunda şu şekilde bulunur:

h = L \cdot \sin(30^\circ)

Buradan da (h = L \cdot \frac{1}{2}) elde edilir.

2. Bitiş Durumu ((\theta = 0^\circ)) Enerji Hesapları:

Kinetik Enerji ve Yay Enerjisi:

Çubuğun dönme kinetik enerjisi:

K = \frac{1}{2} I_G \cdot \omega^2

Burada (I_G), çubuğun dönme atalet momentidir ve ince bir çubuk için:

I_G = \frac{1}{12} m L^2

Yayın sıkışma enerjisi ((U_f)):

U_f = \frac{1}{2} k x_f^2

3. Enerji Korunumu:

Enerji korunumu prensibi, başlangıçtaki tüm enerjinin bitişteki toplam enerjiye eşit olduğunu belirtir:

m \cdot g \cdot L \cdot \sin(30^\circ) = \frac{1}{2} I_G \cdot \omega^2 + \frac{1}{2} k x_f^2

Çubuğun uzunluğu ((L)), kütlesi ((m)) ve yay katsayısı ((k)) verilmiştir; bu parametrelerle enerji denklemi ile ilerlenir ve (\omega) açısal hızı hesaplanır.

Bu şekilde formülleri daha açık hale getirdim. Eğer başka bir konuda yardıma ihtiyacınız varsa, lütfen bana bildirin!